Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

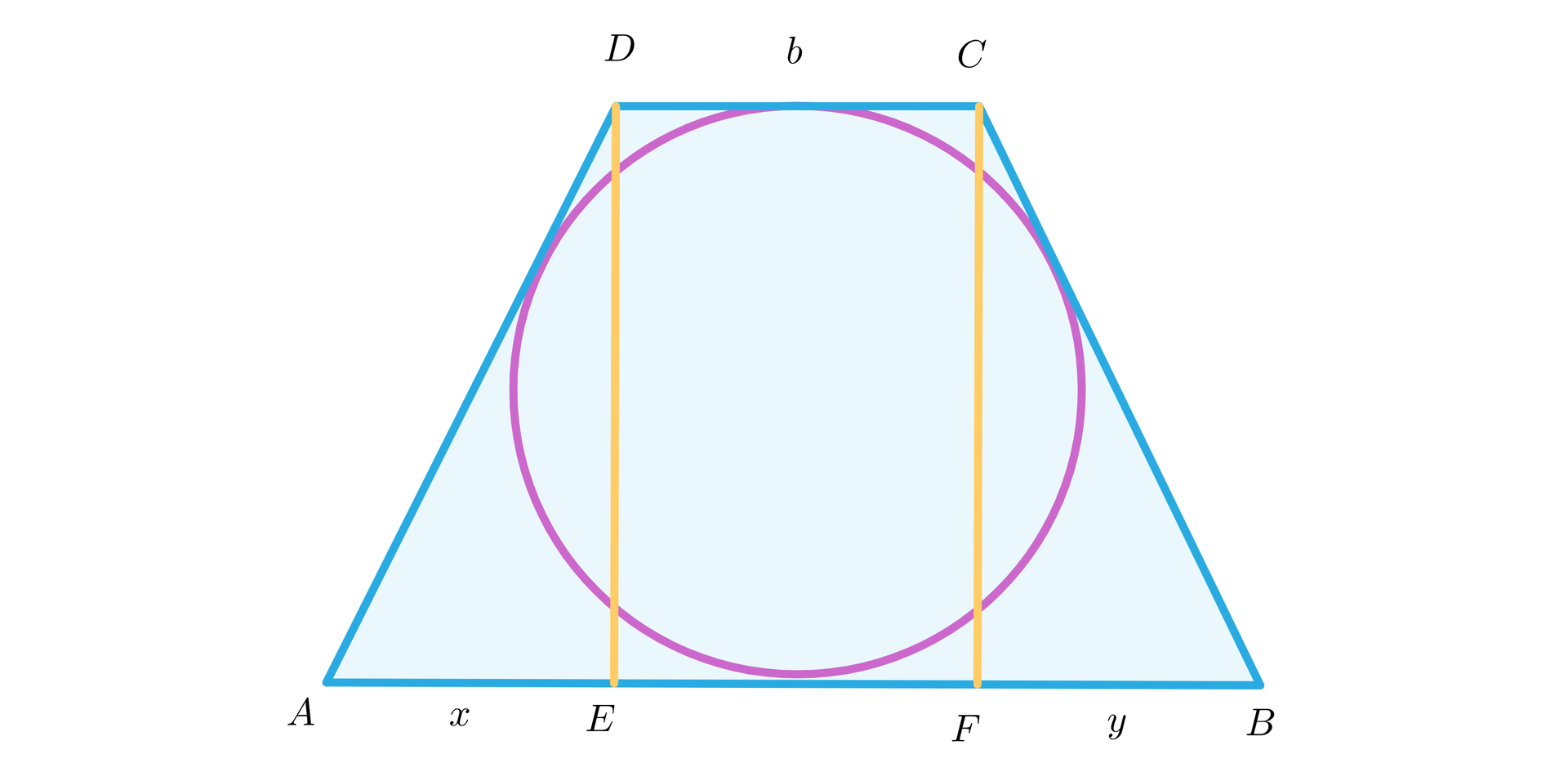
Dłuższa podstawa $A B$ trapezu równoramiennego $A B C D$ opisanego na okręgu o promieniu $3$ jest równa $18$ . Oblicz pole trapezu.

Oznaczmy przez $b$ długość krótszej podstawy, a przez $c$ długość ramienia trapezu. Wtedy, korzystając z twierdzenia o czworokącie opisanym na okręgu mamy, że $2 c = 18 + b$ .

Wysokość trapezu, poprowadzona z wierzchołka krótszej podstawy, jest równa $6$ i jest przyprostokątną w trójkącie prostokątnym, w którym przeciwprostokątną jest równa $c$ , a druga przyprostokątna ma długość $\frac{18 - b}{2}$ .

Korzystając z twierdzenia Pitagorasa otrzymujemy: $6^{2} + {(\frac{18 - b}{2})}^{2} = {(\frac{18 + b}{2})}^{2}$ . Po zastosowaniu wzoru skróconego mnożenia i redukcji otrzymujemy, że $18 b = 36$ , czyli $b = 2$ . Zatem pole jest równe $P = \frac{18 + 2}{2} \cdot 6 = 60$ .

Ćwiczenie 2

W deltoidzie $A B C D$ krótszy bok ma długość $4$ , a dwa przeciwległe kąty mają miary odpowiednio $60 °$ i $120 °$ . Oblicz promień okręgu wpisanego w ten deltoid.

Zauważmy, że dwa pozostałe kąty deltoidu są proste, a oś symetrii dzieli ten deltoid na dwa trójkąty prostokątne, których kąty ostre mają miary $60 °$ i $30 °$ .

Dłuższy bok deltoidu (dłuższa przyprostokątna każdego z otrzymanych trójkątów) ma długość $4 \sqrt{3}$ , stąd pole deltoidu, jako suma pól dwóch przystających trójkątów prostokątnych jest równe $P = 2 (\frac{1}{2} \cdot 4 \cdot 4 \sqrt{3}) = 16 \sqrt{3}$ .

Ale pole czworokąta opisanego na okręgu można wyrazić jako iloczyn promienia $r$ tego okręgu i połowy obwodu, zatem $16 \sqrt{3} = \frac{(2 \cdot 4 + 2 \cdot 4 \sqrt{3}) \cdot r}{2}$ . Stąd otrzymujemy, że $r = \frac{16 \sqrt{3}}{4 + 4 \sqrt{3}} = 6 - 2 \sqrt{3}$ .

R1SA8Ctqyiaa31

Ćwiczenie 3

RgqZYYacO88k92

Ćwiczenie 4

Ćwiczenie 5

RCetstyZW3MGA

R1cGpjvbBUlch

W czworokąt o bokach długości a, b, c, d można wpisać okrąg. Długości boków tego czworokąta, w zależności od x, są opisane na rysunkach. Dopasuj zależności do wartości x. x, równa się, dwa Możliwe odpowiedzi: 1. Ilustracja przedstawia okrąg wpisany w czworokąt. Boki czworokąta wynoszą. a, równa się, trzy x, plus, jeden, b, równa się, dwa x, plus, jeden, c, równa się, x, plus, trzy oraz d, równa się, cztery x, minus, trzy., 2. Ilustracja przedstawia okrąg wpisany w czworokąt. Boki czworokąta wynoszą. a, równa się, cztery x, plus, jeden, b, równa się, dwa x, plus, dwa, c, równa się, cztery x, minus, trzy oraz d, równa się, pięć x, minus, dwa., 3. Ilustracja przedstawia okrąg wpisany w czworokąt. Boki czworokąta wynoszą. a, równa się, x indeks górny, dwa, koniec indeksu górnego, minus, x, minus, jeden, b, równa się, dwa x, plus, jeden, c, równa się, dwa x oraz d, równa się, dwa x indeks górny, dwa, koniec indeksu górnego, minus, siedem x, plus, sześć. x, równa się, trzy Możliwe odpowiedzi: 1. Ilustracja przedstawia okrąg wpisany w czworokąt. Boki czworokąta wynoszą. a, równa się, trzy x, plus, jeden, b, równa się, dwa x, plus, jeden, c, równa się, x, plus, trzy oraz d, równa się, cztery x, minus, trzy., 2. Ilustracja przedstawia okrąg wpisany w czworokąt. Boki czworokąta wynoszą. a, równa się, cztery x, plus, jeden, b, równa się, dwa x, plus, dwa, c, równa się, cztery x, minus, trzy oraz d, równa się, pięć x, minus, dwa., 3. Ilustracja przedstawia okrąg wpisany w czworokąt. Boki czworokąta wynoszą. a, równa się, x indeks górny, dwa, koniec indeksu górnego, minus, x, minus, jeden, b, równa się, dwa x, plus, jeden, c, równa się, dwa x oraz d, równa się, dwa x indeks górny, dwa, koniec indeksu górnego, minus, siedem x, plus, sześć. x, równa się, cztery Możliwe odpowiedzi: 1. Ilustracja przedstawia okrąg wpisany w czworokąt. Boki czworokąta wynoszą. a, równa się, trzy x, plus, jeden, b, równa się, dwa x, plus, jeden, c, równa się, x, plus, trzy oraz d, równa się, cztery x, minus, trzy., 2. Ilustracja przedstawia okrąg wpisany w czworokąt. Boki czworokąta wynoszą. a, równa się, cztery x, plus, jeden, b, równa się, dwa x, plus, dwa, c, równa się, cztery x, minus, trzy oraz d, równa się, pięć x, minus, dwa., 3. Ilustracja przedstawia okrąg wpisany w czworokąt. Boki czworokąta wynoszą. a, równa się, x indeks górny, dwa, koniec indeksu górnego, minus, x, minus, jeden, b, równa się, dwa x, plus, jeden, c, równa się, dwa x oraz d, równa się, dwa x indeks górny, dwa, koniec indeksu górnego, minus, siedem x, plus, sześć.

Ćwiczenie 6

Przeprowadź konstrukcję czworokąta, który można opisać na okręgu, mając dany bok $a$ , kąty wewnętrzne $α$ , $β$ , którego ramiona zawierają dany bok $a$ oraz trzeci kąt tego czworokąta $γ$ .

Na prostej odkładamy odcinek $a$ - otrzymujemy wierzchołki $A$ , $B$ czworokąta.
Odkładamy kąt odpowiednio o mierze $α$ w wierzchołku $A$ i o mierze $β$ w wierzchołku $B$ tak, aby ich jedno ramię zawierało odcinek $a$ , a drugie ramiona leżały po tej samej stronie prostej – otrzymujemy półproste $k$ i $l$ zawierające boki czworokąta przyległe do boku $a$ .
Kreślimy dwusieczne kątów $α$ i $β$ - otrzymujemy środek $O$ okręgu wpisanego.
Kreślimy prostą prostopadłą do odcinka $a$ przechodzącą przez punkt $O$ - w punkcie przecięcia tej prostopadłej i odcinka otrzymujemy punkt styczności $E$ .
Kreślimy okrąg o środku w punkcie $O$ i promieniu $|O E|$ .
Na półprostej $l$ (lub $k$ ), w dowolnym punkcie, jako wierzchołku, odkładamy kąt $γ$ - otrzymujemy półprostą $m$ , która jest równoległa do boku $C D$ czworokąta.
Kreślimy styczną do skonstruowanego wcześniej okręgu równoległą do półprostej $m$ . W tym celu prowadzimy prostą prostopadłą do $m$ i przechodzącą przez środek okręgu $O$ - otrzymany punkt wspólny prostej i okręgu jest punktem styczności, przez który prowadzimy prostopadłą.

RoQgqXn19ezcx

Ilustracja przedstawia fragment czworokąta z widocznym wierzchołkiem A i B. Bok A B tworzy podstawę tego czworokąta . Przy wierzchołku A odłożoną kąt o mierze alfa tak aby jedno ramie leżało na odcinku AB a drugie tworzyło ramie czworokąta k. Przy wierzchołku B odłożono kąt o mierze beta tak że jedno ramie pokrywa się z odcinkiem A B a drugie ramie wyznacza ramie czworokąta l. Poprowadzone są półproste wyznaczające dwusieczne podanych kątów. Ich miejsce przecięcia oznaczono punktem O. Następnie poprowadzona jest prosta prostopadła do boku A B przechodząca przez punkt O. Miejsce przecięcia tej prostej z bokiem A B oznaczono punktem E. Wykreślony jest również okrąg o promieniu długości O E, który jest styczny do punktu E i ramion czworokąta k i l. Na półprostej l odłożono kąt gamma powyżej okręgu tak że jedno ramie pokrywa się z półprostą l a drugie tworzy półprostą m. Wyznaczono również styczną do okręgu równoległą do prostej m.

Ćwiczenie 7

Na okręgu o promieniu $5$ opisano trapez, którego ramiona mają długości: $|A D| = 12, 5$ , $|B C| = 10, 3$ . Wyznacz długość krótszej podstawy tego trapezu.

Przyjmijmy oznaczenia, jak na rysunku.

RKRuY064NKNia

Ilustracja przedstawia okrąg wpisany w trapez ABCD. Zaznaczono wysokości upuszczone na dłuższa podstawę, wysokości o odcinkach DE i CF. Podstawa DC ma długość b, odcinek AE ma długość x, a odcinek BF długość y.

Wtedy mamy: ${(12 \frac{1}{2})}^{2} = x^{2} + 10^{2}$ , ${(10 \frac{3}{10})}^{2} = y^{2} + 10^{2}$ oraz $x + y + 2 b = 12 \frac{1}{2} + 10 \frac{3}{10}$ .

Zatem $x = \sqrt{{(12 \frac{1}{2})}^{2} - 10^{2}} = 7 \frac{1}{2}$ oraz $y = \sqrt{{(10 \frac{3}{10})}^{2} - 10^{2}} = \frac{\sqrt{609}}{10}$ .

Otrzymujemy więc, że $b = \frac{12 \frac{1}{2} + 10 \frac{3}{10} - x - y}{2} = \frac{12 \frac{1}{2} + 10 \frac{3}{10} - 7 \frac{1}{2} - \frac{\sqrt{609}}{10}}{2} = \frac{153 - \sqrt{609}}{20}$ .

Rh8mHwfkmkABY3

Ćwiczenie 8

Aplet

Dla nauczyciela