Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

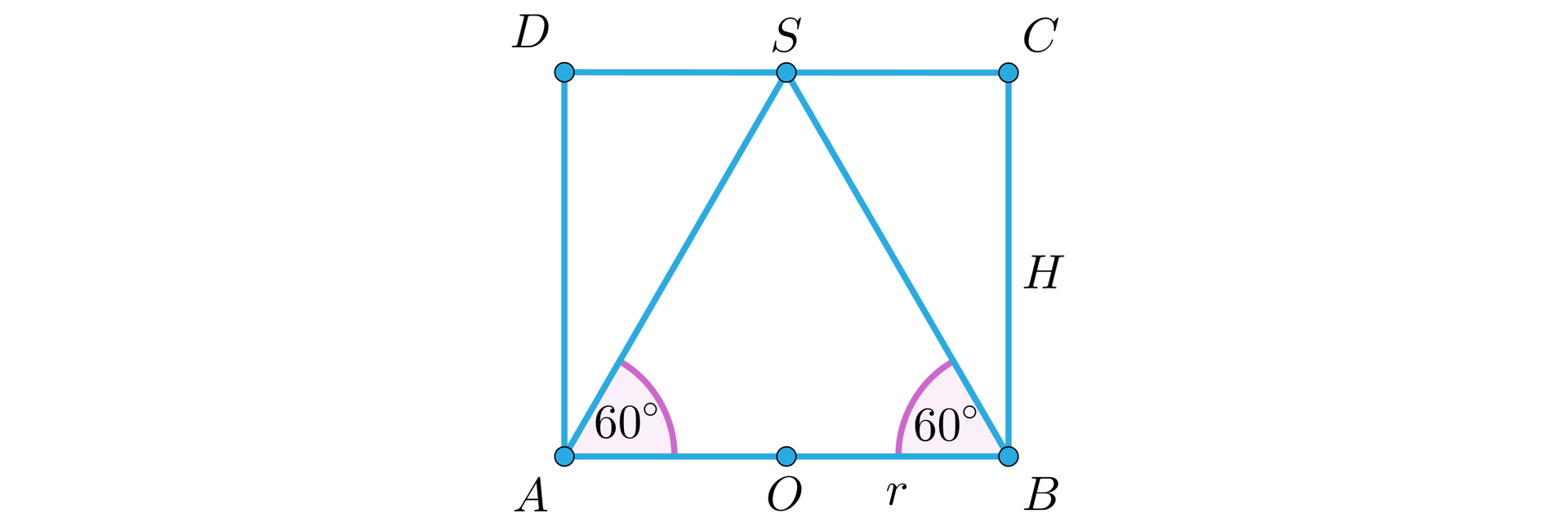
Dany jest walec opisany na stożku. Przekrój osiowy tego stożka jest trójkątem równobocznym o polu powierzchni równym $147 \sqrt{3} {cm}^{2}$ . Oblicz objętość walca opisanego na tym stożku. W rachunkach przyjmij $π = \frac{22}{7}$ . Wpisz odpowiedź.

R1af6VGe4Me8r

Na ilustracji przedstawiono prostokąt ABCD. Punkt S stanowi środek boku CD, natomiast punkt O stanowi środek boku AB. Długość odcinka OB oznaczono literą r. Zaznaczono trójkąt równoboczny ABS oraz jego kąty wewnętrzne wynoszące 60 stopni.

R1TsbyAs6511b

$V =$ ............ ${cm}^{3}$

R9qhbFOBilHdW1

Ćwiczenie 2

W walec wpisano stożek. Wiedząc, że stosunek pola powierzchni bocznej walca do pola powierzchni bocznej stożka wynosi $1 : 1$ . Wybierz wszystkie zdania prawdziwe.

długość wysokości walca jest dwa razy mniejsza od długości tworzącej stożka
długość wysokości walca jest dwa razy większa od długości tworzącej stożka
pole powierzchni całkowitej stożka i walca są takie same
kąt rozwarcia stożka ma miarę $120 °$

Ćwiczenie 3

R13k3J2kKH3Qq

RL3lcYM4zpZP5

RRxvqKsOK0FZJ2

Ćwiczenie 4

Stosunek długości wysokości walca do długości tworzącej stożka wpisanego w ten walec wynosi $\frac{1}{2}$ , wynika stąd, że miara kąta rozwarcia stożka wynosi:

$120 °$
$60 °$
$30 °$
$150 °$

Ćwiczenie 5

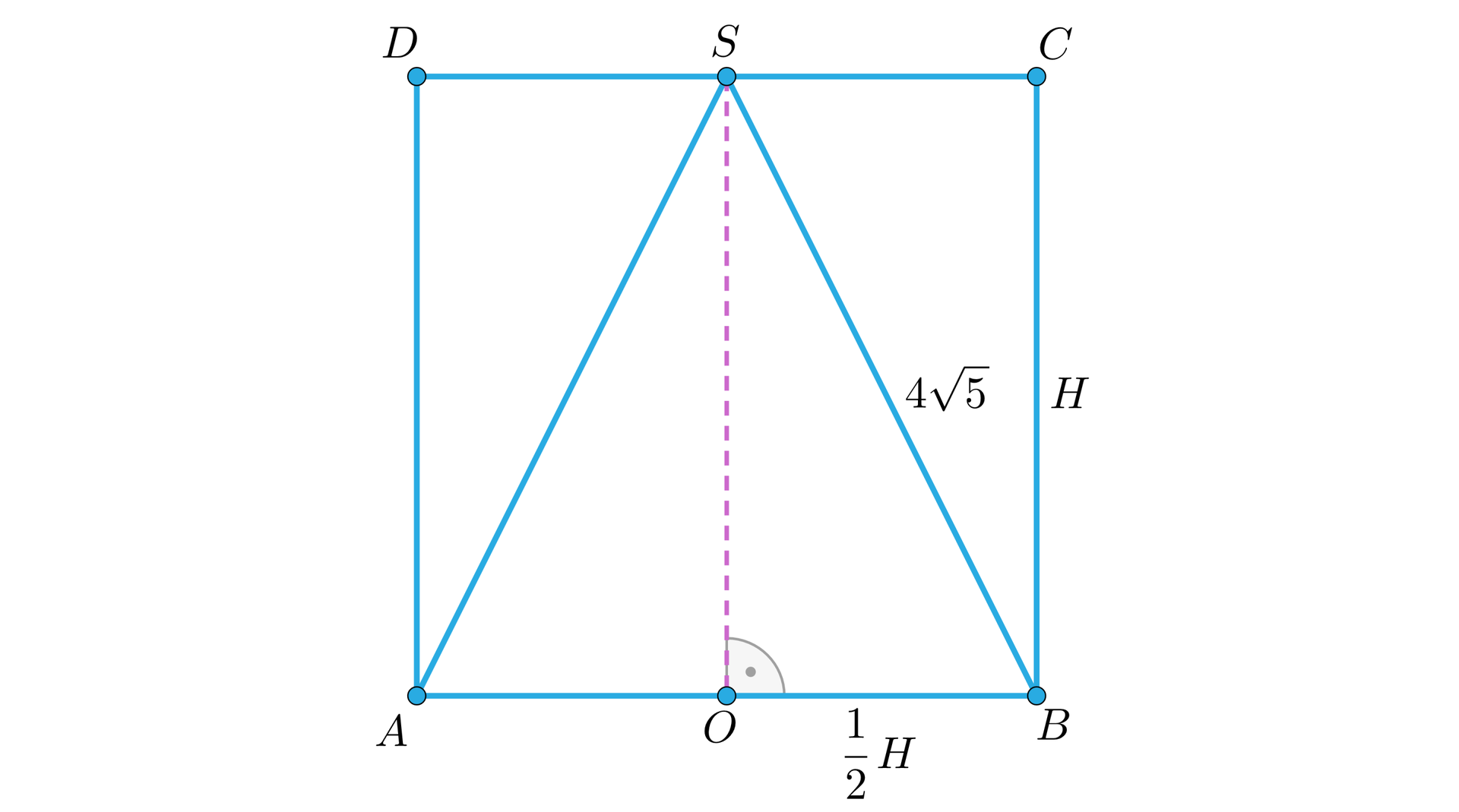
Dany jest walec opisany na stożku. Przekrojem osiowym tego walca jest kwadrat, natomiast długość tworzącej tego stożka wynosi $4 \sqrt{5} cm$ . Oblicz objętość walca.

R14Fg0cpb8Khm

Na ilustracji przedstawiono kwadrat ABCD o boku długości H. Zaznaczono punkty stanowiące środki przeciwległych boków. Punkt S na boku CD oraz punkt O na boku AB. Zaznaczono trójkąt ASB, którego ramię ma długość 45. Linią przerywaną zaznaczono odcinek łączący punkty S i O, prostopadły do boku AB.

Z twierdzenia Pitagorasa dla trójkąta $O B S$ mamy $H^{2} + {(\frac{1}{2} H)}^{2} = {(4 \sqrt{5})}^{2}$ , stąd $H = 8$ i $r = 4$ .

Objętość walca obliczymy ze wzoru $V_{w} = π r^{2} H = 128 π [{cm}^{3}]$ .

Ćwiczenie 6

Kąt rozwarcia stożka wpisanego w walec ma miarę $150 °$ . Wiedząc, że długość średnicy podstawy walca wynosi $8 cm$ , oblicz objętość walca.

Wykreślamy przekrój osiowy odpowiednich brył i przyjmujemy oznaczenia jak na rysunku:

RBLAV7JmgFMpo

Na ilustracji przedstawiono prostokąt ABCD. Zaznaczono punkty stanowiące środki dłuższych boków. Punkt S na boku CD oraz punkt O na boku AB. Zaznaczono trójkąt ASB, którego długość ramienia oznaczono literą l. Linią przerywaną zaznaczono wysokość trójkąta oznaczoną H, która łączy punkty S i O. ∠ASB wynosi alfa, natomiast długość odcinka OB oznaczono literą r.

Z twierdzenia cosinusów dla trójkąta $A B S$ mamy zależność ${(2 r)}^{2} = 2 l^{2} - 2 l^{2} \cos α$ , po podstawieniu otrzymujemy $8^{2} = 2 l^{2} - 2 l^{2} \cos 150 °$ , stąd $64 = 2 l^{2} (1 + \frac{\sqrt{3}}{2})$ , zatem $l = 8 \sqrt{2 - \sqrt{3}}$ . Ponieważ z twierdzenia Pitagorasa dla trójkąta $O B S$ otrzymujemy $H^{2} + r^{2} = l^{2}$ , stąd $H^{2} = 64 (2 - \sqrt{3}) - 16$ , zatem $H = 4 \sqrt{7 - 4 \sqrt{3}}$ . Objętość walca obliczamy ze wzoru $V = π r^{2} H = π \cdot 16 \cdot 4 \sqrt{7 - 4 \sqrt{3}} = 64 \sqrt{7 - 4 \sqrt{3}} π [{cm}^{3}]$ .

Ćwiczenie 7

W walec wpisano stożek. Stosunek pola powierzchni bocznej walca do pola powierzchni bocznej stożka wynosi $\frac{2}{3}$ . Wyznacz cosinus kąta rozwarcia stożka.

R1K2R2OCgThhR

Na ilustracji przedstawiono prostokąt ABCD. Zaznaczono punkty stanowiące środki krótszych boków. Punkt S na boku CD oraz punkt O na boku AB. Zaznaczono trójkąt ASB, którego długość ramienia oznaczono literą l. Linią przerywaną zaznaczono wysokość trójkąta oznaczoną H, która łączy punkty S i O. Długość odcinka OB oznaczono literą r.

Przyjmujemy oznaczenia.

$|O B| = r$ długość podstawy stożka i walca,

$|O S| = H$ długość wysokości walca i stożka,

$|B S| = l$ długość tworzącej stożka.

Kąt rozwarcia stożka, który mamy wyznaczyć to $∢ A S B$ . Przyjmijmy, że miara $|∢ A S B| = α$ .

Z warunków zadania mamy $\frac{P_{b w}}{P_{b s}} = \frac{2 H}{l} = \frac{2}{3}$ , zatem $l = 3 H$ .

Z twierdzenia Pitagorasa dla trójkąta $O B S$ mamy $H^{2} + r^{2} = {(3 H)}^{2}$ , stąd $r = 2 \sqrt{2} H$ .

Do wyznaczenia cosinusa kąta rozwarcia stożka możemy wykorzystać albo twierdzenie cosinusów dla trójkąta $A B S$ : ${(2 r)}^{2} = 2 l^{2} - 2 l^{2} \cos α$ albo zależność dla cosinusa kąta podwojonego wyznaczając cosinus kąta $O S B$ .

$\cos α = - \frac{7}{9}$

Ćwiczenie 8

W walcu, wydrążono stożek o średnicy podstawy długości $a$ i wysokości długości dwa razy dłuższej od średnicy podstawy stożka. Przekrój osiowy walca po wydrążeniu stożka przedstawiono na rysunku.

R1QKxI6hs0s55

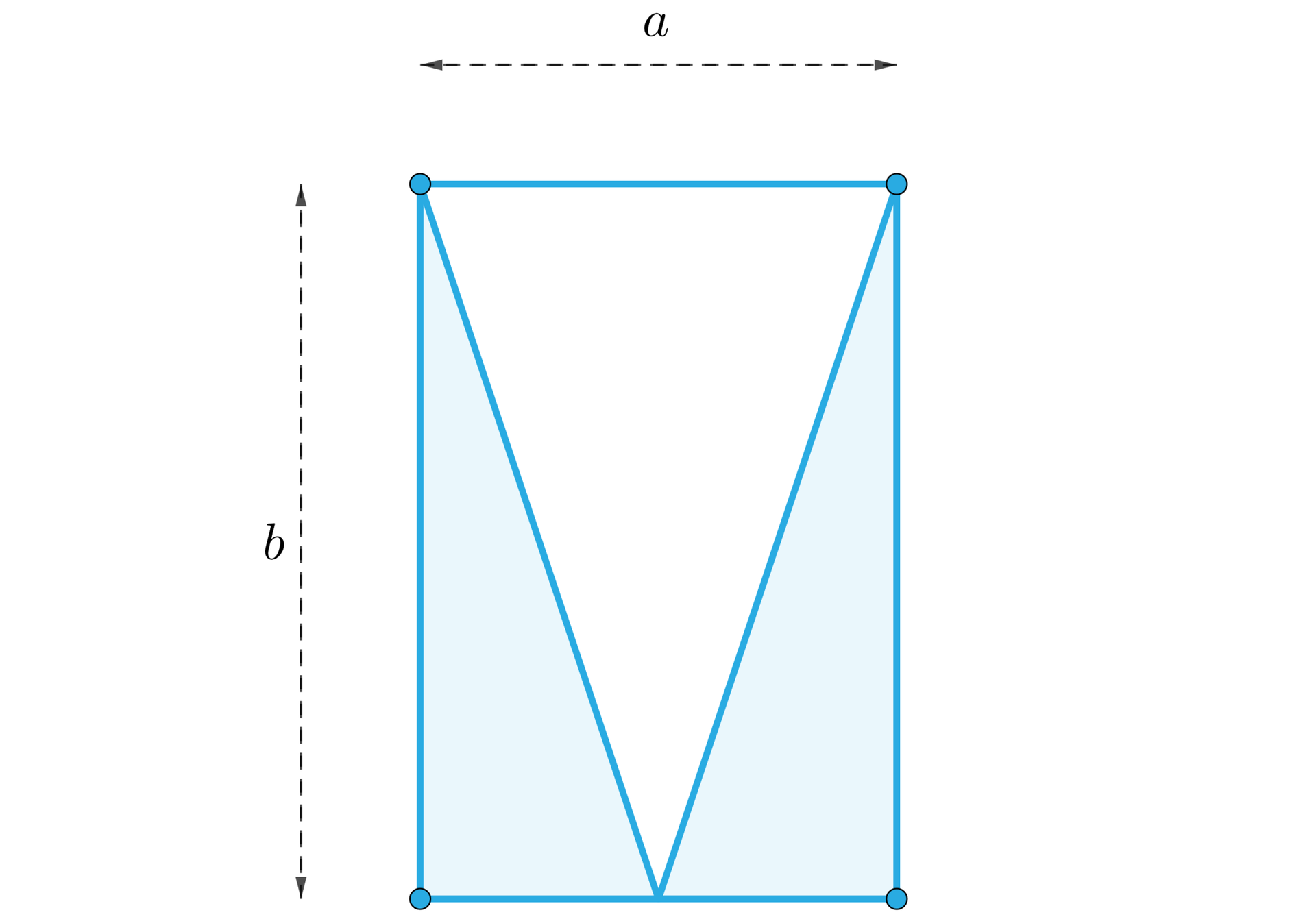
Na ilustracji przedstawiono prostokąt. Długość krótszego boku oznaczono literą a, natomiast długość boku dłuższego oznaczono literą b. Wewnątrz prostokąta znajduje się trójkąt, którego wierzchołek leży na krótszym boku prostokąta, natomiast podstawa trójkąta pokrywa się z długością przeciwległego krótszego boku prostokąta.

Wierzchołek stożka znajduje się na powierzchni podstawy walca. Oblicz pole całkowite powierzchni bryły pozostałej z walca po wydrążeniu stożka.

Z warunków zadania mamy $b = 2 a$ .

Pole powierzchni części walca pozostałej po wydrążeniu stożka jest sumą pól powierzchni jednej podstawy walca, pola powierzchni bocznej walca oraz pola powierzchni bocznej stożka.

Mamy zatem $P_{c} = π {(\frac{1}{2} a)}^{2} + 2 π \cdot \frac{1}{2} a \cdot 2 a + π \cdot \frac{1}{2} a \cdot l$ , gdzie $l$ oznacza długość tworzącej stożka.

Długość tworzącej stożka obliczmy odpowiednio z twierdzenia Pitagorasa $l^{2} = {(2 a)}^{2} + {(\frac{1}{2} a)}^{2}$ , stąd $l = \frac{\sqrt{17}}{2} a$ .

Zatem $P_{c} = \frac{π}{4} a^{2} + 2 π a^{2} + π \cdot \frac{\sqrt{17}}{4} a^{2} = \frac{9 + \sqrt{17}}{4} π a^{2}$ .

Aplet

Dla nauczyciela