Symulacja interaktywna
Polecenie 1
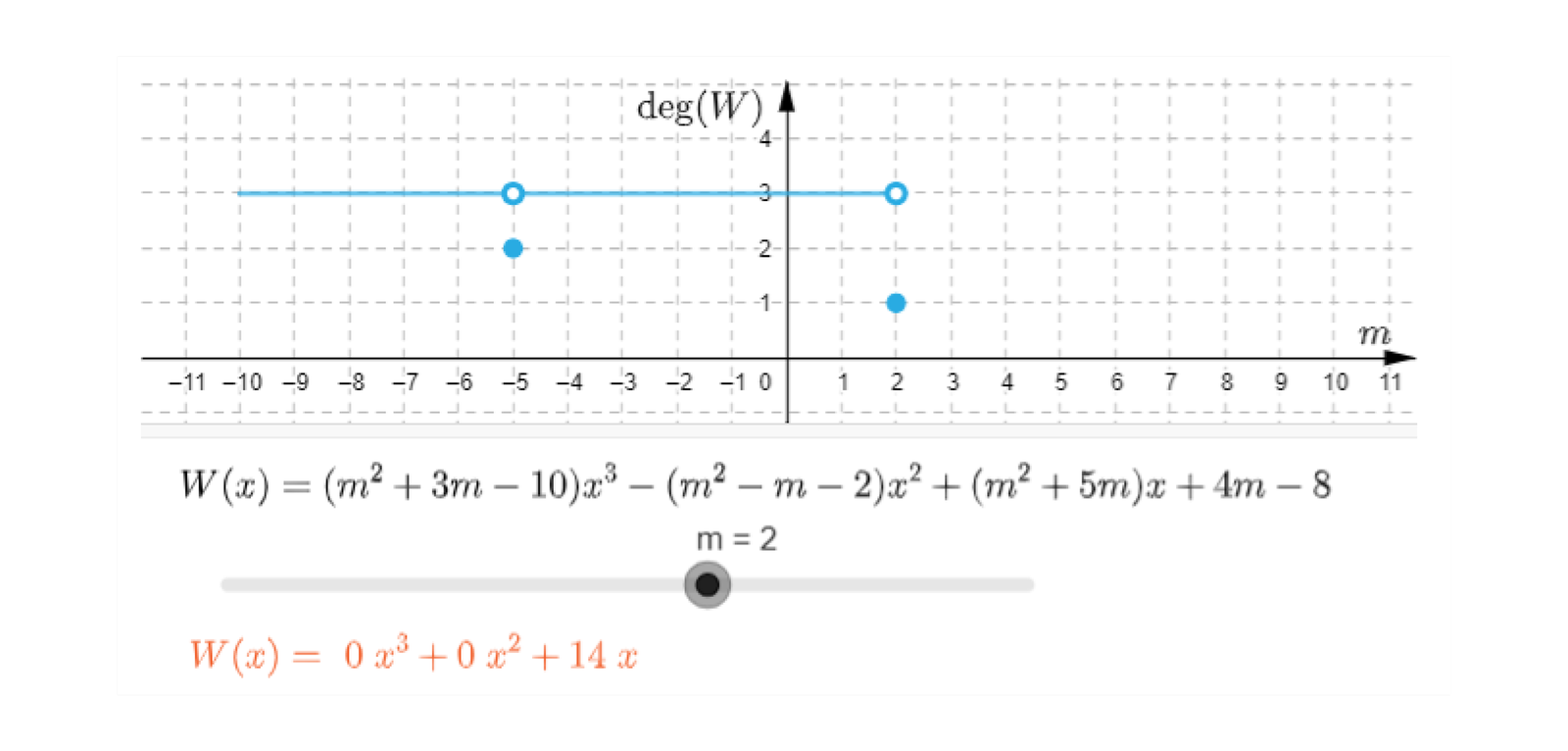
W zadaniach z funkcją kwadratową często pojawiał się parametr. Podobnie może być przy wielomianach stopnia innego niż .
Przeanalizuj, jak zmieniają się współczynniki podanego wielomianu w zależności od parametru . Zobacz, jakie wartości może przyjmować stopień wielomianu.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DmGdGCitw
Polecenie 2
- Wielomian może być co najwyżej stopnia trzeciego.
- Dla parametru wielomian jest stopnia trzeciego.
- Dla parametru wielomian jest stopnia drugiego.
- Nie ma takiego parametru , dla którego wielomian jest stopnia pierwszego.
- Dla parametru wielomian jest wielomianem zerowym.
Polecenie 3
Ustal stopień wielomianu w zależności od parametru .
Polecenie 4
Ustal, jaki jest stopień wielomianu w zależności od parametru .