Wartość bezwzględna - definicja
Niech będzie dowolną liczbą rzeczywistą.
Odległość liczby od liczby na osi liczbowej nazywamy wartością bezwzględną liczby .
Wartość bezwzględną liczby oznaczamy .
Zauważmy, że z definicji wartości bezwzględnej wynikają jej własności:
wartość bezwzględna liczby jest dodatnia lub równa , czyli
, dla dowolnej liczby rzeczywistej ,
jeśli , to ,
wartości bezwzględne liczb przeciwnych są równe, czyli
dla dowolnej liczby rzeczywistej .
Film dostępny na portalu epodreczniki.pl
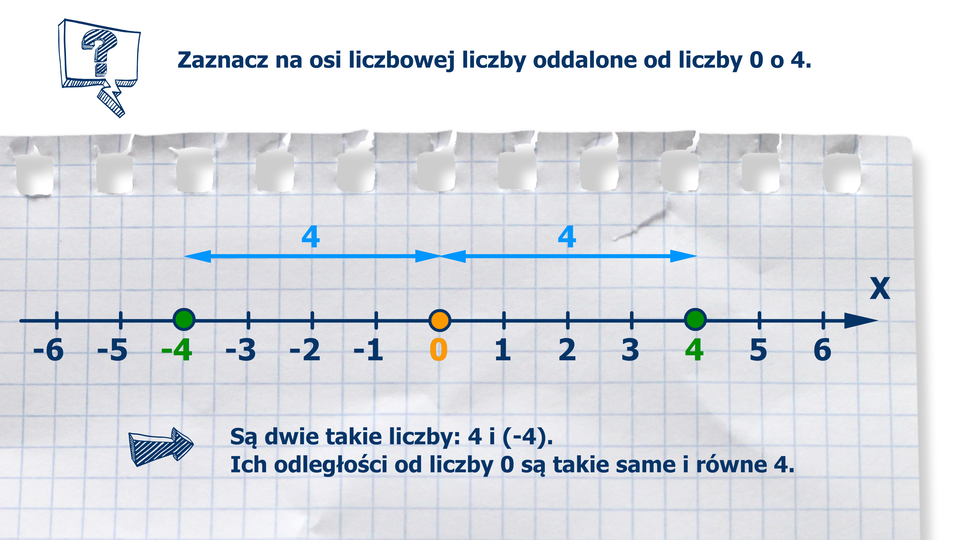
Animacja przedstawia oś liczbową z zaznaczonymi punktami od -6 do 6. Należy zaznaczyć liczby oddalone od liczby 0 o 4. Są dwie takie liczby: 4 i -4. Ich odległości od liczby 0 są takie same i wynoszą 4.

Film dostępny na portalu epodreczniki.pl
Animacja pokazuje rozwiązanie równania: wartość bezwzględna z liczby x =a, gdzie a większe lub równe 0. Szukamy takich liczb, których odległość od liczby 0 jest równa a. Na osi zaznaczona odległość liczby a od liczby 0, równa a oraz odległość liczby –a od liczby 0, równa a. Zapis: Niech a większe lub równe 0. Rozwiązaniem równania wartość bezwzględna z liczby x =a jest x =a lub x =-a.
Zaznacz na osi liczbowej liczby spełniające równanie.

Film dostępny na portalu epodreczniki.pl
Animacja pokazuje na osi liczbowej rozwiązanie nierówności: wartość bezwzględna z liczby x <a, gdzie a większe lub równe 0. Szukamy takich liczb, których odległość od liczby 0 jest mniejsza od a. Na osi zaznaczona odległość liczby a od liczby 0, równa a oraz odległość liczby –a od liczby 0, równa a. Zapis: Niech a większe lub równe 0. Rozwiązaniem nierówności wartość bezwzględna z liczby x <a jest przedział (-a, a).

Film dostępny na portalu epodreczniki.pl
Animacja przedstawia oś liczbową z zaznaczonymi punktami od -6 do 6. Należy znaleźć na osi liczbowej wszystkie liczby, których odległość od liczby 0 jest mniejsza niż 4. W tym celu na osi liczbowej zaznaczamy odległości od liczby 0 liczb -4 i 4, równe 4. Liczby, których odległość od 0 jest mniejsza niż 4 należą do przedziału(-4, 4). Możemy zatem powiedzieć, że przedział (-4, 4) zawiera liczby, które spełniają nierówność wartość bezwzględna z liczby x <4.

Film dostępny na portalu epodreczniki.pl
Animacja pokazuje na osi liczbowej rozwiązanie nierówności: wartość bezwzględna z liczby x >a, gdzie a większe lub równe 0. Szukamy takich liczb, których odległość od liczby 0 jest większa od a. Na osi zaznaczona odległość liczby a od liczby 0, równa a oraz odległość liczby –a od liczby 0, równa a. Zapis: Niech a większe lub równe 0. Rozwiązaniem nierówności wartość bezwzględna z liczby x > a jest suma przedziałów (minus nieskończoność, -a) i (a, plus nieskończoność).

Film dostępny na portalu epodreczniki.pl
Animacja przedstawia oś liczbową z zaznaczonymi punktami od -6 do 6. Należy znaleźć na osi liczbowej wszystkie liczby, których odległość od liczby 0 jest większa niż 4. W tym celu na osi liczbowej zaznaczamy odległości od liczby 0 liczb -4 i 4, równe 4. Liczby, których odległość od 0 jest większa niż 4 należą do sumy przedziałów (minus nieskończoność, -4) i (4, plus nieskończoność). Możemy zatem powiedzieć, że zbiór przedziałów (minus nieskończoność, -4) i (4, plus nieskończoność) zawiera liczby, które spełniają nierówność wartość bezwzględna z liczby x >4.
Wartość bezwzględna liczby jest przydatna do definiowania odległości miedzy liczbami na osi liczbowej.
Oblicz odległość na osi liczbowej liczb i .

Film dostępny na portalu epodreczniki.pl
Animacja przedstawia zaznaczoną na osi liczbowej odległość między liczbami 9 oraz dwa i jedna druga. Zapis: wartość bezwzględna z liczby (9 – dwa i jedna druga) = wartość bezwzględna z liczby (dwa i jedna druga -9) = sześć i jedna druga.
Odległość między tymi liczbami obliczyliśmy, odejmując mniejszą z nich od większej, czyli
Odległość jest zawsze liczbą nieujemną. Ponieważ nie zawsze możemy łatwo stwierdzić, która z danych liczb jest większa, a która mniejsza, wykorzystamy wartość bezwzględną.
Oblicz odległość na osi liczbowej liczb i .

Film dostępny na portalu epodreczniki.pl
Animacja przedstawia zaznaczoną na osi liczbowej odległość między liczbami -1 oraz siedem i jedna druga. Zapis: wartość bezwzględna z liczby [siedem i jedna druga -(-1)] = wartość bezwzględna z liczby (-1, siedem i jedna druga) = osiem i jedna druga.
Odległość liczb i na osi liczbowej jest równa wartości bezwzględnej ich różnicy .
Zapis możemy czytać następująco: odległość liczby od liczby na osi liczbowej jest równa .
Zaznacz na osi liczbowej liczby, które spełniają równanie
Aby rozwiązać równanie, należy znaleźć takie liczby , których odległość na osi liczbowej od jest równa .

Film dostępny na portalu epodreczniki.pl
Animacja przedstawia na osi liczbowej rozwiązanie równania: wartość bezwzględna z liczby x -2 =4. Szukamy takiej liczby x, której odległość na osi liczbowej od liczby 2 wynosi 4. W tym celu zaznaczamy na osi punkt o współrzędnej 2. Od liczby 2 zaznaczamy odległość 4 do liczb -2 i 6. Szukane liczby to x z indeksem dolnym jeden =-2 i x z indeksem dolnym dwa =6.
Korzystając z interpretacji geometrycznej nierówności, zauważamy, że w odległości od liczby znajdują się liczby i . Są to liczby spełniające równanie.
Wyznacz liczby, które są rozwiązaniem nierówności

Film dostępny na portalu epodreczniki.pl
Animacja przedstawia na osi liczbowej rozwiązanie nierówności: wartość bezwzględna z liczby (x -1) mniejsza lub równa 4. Szukamy takich liczb x, której odległość na osi liczbowej od liczby 1 jest mniejsza lub równa 4. W tym celu zaznaczamy na osi punkt o współrzędnej 1. Od liczby 1 zaznaczamy odległość 4 do liczb -3 i 5. Szukane liczby należą do przedziału <-3, 5>.
Korzystając z interpretacji geometrycznej nierówności, zauważamy, że nierówność spełniają liczby należące do przedziału .
Wyznacz liczby, które są rozwiązaniem nierówności
Jeśli nierówność zapiszemy jako , to będzie można ją odczytać: odległość liczby od liczby jest większa od .
Zaznaczymy liczby spełniające nierówność na osi liczbowej.

Film dostępny na portalu epodreczniki.pl
Animacja przedstawia na osi liczbowej rozwiązanie nierówności: wartość bezwzględna z liczby (x +1) >3. Wartość bezwzględna z liczby [x –(-1)] >3. Szukamy takich liczb x, której odległość na osi liczbowej od liczby 1 jest większa od 3. W tym celu zaznaczamy na osi punkt o współrzędnej -1. Od liczby -1 zaznaczamy odległość 3 do liczb -4 i 2. Szukane liczby należą do sumy przedziałów (minus nieskończoność, -4) i (2, plus nieskończoność).
Nierówność spełniają wszystkie liczby należące do sumy przedziałów .
Połącz w pary nierówności z odpowiednimi opisami słownymi.
odległość liczby x od liczby (-2) jest nie większa niż 7, odległość liczby x od liczby 7 jest nie większa niż 2, odległość liczby x od liczby 7 jest większa od 2, odległość liczby x od liczby (-7) jest większa od 2, odległość liczby x od liczby (-7) jest mniejsza lub równa 2, odległość liczby x od liczby 2 jest mniejsza lub równa 7
Rozwiązaniem nierówności jest zbiór
Liczby spełniające równanie to
- oraz
- oraz
- oraz
- oraz
Rozwiązaniem nierówności jest przedział
Przeciągnij i upuść.
, , ,
Przedział (-3,5) jest rozwiązaniem nierówności .................
Liczba należy do przedziału
Równanie spełnia liczba należąca do przedziału
Liczba spełnia warunek
Rozwiązaniem nierówności jest przedział
Liczba należy do przedziału
Liczby należące jednocześnie do przedziałów i przedstawione są na rysunku.
- 16462
- 16463
- 16464
- 16465




Ile liczb całkowitych należy do przedziału ?
Dane są liczby oraz . Liczba należy do przedziału
Wskaż nierówność, którą spełniają liczby należące do przedziału zaznaczonego na rysunku.

Które zdanie jest prawdziwe?
- Liczba spełnia nierówność .
- Liczba spełnia nierówność .
- Liczba spełnia nierówność .
- Liczba spełnia nierówność .
Rozwiąż nierówności.
Rozwiąż nierówności.
Rozwiąż nierówności.
Zapisz przedział, do którego należą wszystkie liczby spełniające warunek
lub
i
Wypisz wszystkie liczby całkowite
należące do przedziału i do przedziału
należące do przedziału i do przedziału
należące do przedziału i do przedziału
należące do przedziału
Zapisz za pomocą układu nierówności zbiór wszystkich liczb, które należą do przedziału
Rozwiąż równanie.
Wyznacz liczby spełniające równanie.
Zaznacz na osi liczbowej i zapisz w postaci przedziału wszystkie liczby spełniające podany warunek.
i i
i


