Funkcja wykładnicza i jej własności. Przekształcanie wykresu funkcji wykładniczej
Zdefiniowaliśmy wcześniej potęgi o wykładnikach naturalnych, całkowitych i wymiernych, przyjmując odpowiednie założenia o podstawach tych potęg.
Powyższą wiedzę uzupełnimy krótką informacją o potędze o wykładniku niewymiernym.
Zakładamy, że podstawa jest liczbą rzeczywistą, dodatnią, wykładnik jest dowolną liczbą niewymierną, na przykład .
Potęga jest liczbą, której przybliżenie możemy znaleźć, przyjmując przybliżenie wymierne wykładnika i ewentualnie podstawy . Oczywiste jest, że im lepsze przybliżenie wykładnika i podstawy, tym dokładniejszą wartość wymierną potęgi otrzymamy. Na przykład:
Korzystając z kalkulatora, otrzymamy:
Możemy teraz przyjąć, że wyrażenie jest dobrze określone dla każdej liczby rzeczywistej i każdej podstawy .
Funkcją wykładniczą nazywamy funkcję określoną dla każdej liczby rzeczywistej wzorem , gdzie jest ustaloną liczbą dodatnią i różną od .
Warunek występujący w tej definicji, dotyczący podstawy wynika z tego, że jedynie dla możemy jednoznacznie określić funkcję dla każdej liczby rzeczywistej . Zauważmy, że dla funkcja nie byłaby określona dla każdej liczby rzeczywistej, np. nie dałoby się obliczyć , gdyż oznaczałoby to konieczność obliczenia pierwiastka kwadratowego z liczby ujemnej, a taki nie istnieje. Dla nie można określić funkcji dla żadnej liczby niedodatniej. Z innego powodu zakładamy, że . Dla funkcja jest, co prawda, określona dla każdej liczby rzeczywistej , ale wówczas jest to funkcja stała
Funkcji nie będziemy uznawać za funkcję wykładniczą, gdyż ma ona inne własności niż każda z funkcji wykładniczych.
Naszkicujmy wykres funkcji określonej dla każdej liczby rzeczywistej wzorem
W tym celu uzupełnijmy tabelę wartościami funkcji dla kilku wybranych argumentów.
Uzupełniamy tabelę, wpisując obliczenia wartości funkcji .
Zastanówmy się, jak funkcja będzie się zachowywać dla bardzo małych argumentów. Na przykład
Jest to liczba dodatnia, ale na tyle mała, że nie uda nam się dokładnie zaznaczyć w układzie współrzędnych punktu , który leży na wykresie tej funkcji. Dla jeszcze mniejszych argumentów wartości funkcji będą nadal dodatnie, ale jeszcze bliższe zeru. Każda, bardzo, bardzo bliska zeru liczba dodatnia jest wartością tej funkcji wykładniczej dla pewnego ujemnego argumentu. Geometrycznie oznacza to, że lewa część wykresu funkcji zbliża się do osi , czyli do prostej o równaniu . Tę prostą nazywamy asymptotą wykresu funkcji.
Krzywa przechodząca przez wyznaczone punkty (te które znaleźliśmy i dowolne inne, które moglibyśmy w ten sposób znaleźć) jest wykresem funkcji wykładniczej . Krzywą taką nazywamy krzywą wykładniczą albo ekspotencjalną.

Przypatrzmy się teraz wykresom innych funkcji wykładniczych
w przypadku, gdy .

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DOgeKo121
Zauważmy, że wszystkie te funkcje są rosnące, a ich wykresy w całości leżą nad osią . Zatem żadna z tych funkcji nie ma miejsca zerowego. Wszystkie wykresy mają jeden wspólny punkt. Jest to punkt o współrzędnych , w którym wykres każdej z tych funkcji przecina oś . Jest tak, ponieważ dla dowolnej liczby mamy .
Rozważmy teraz funkcję określoną dla każdej liczby rzeczywistej wzorem . Korzystając z własności potęg, wzór funkcji możemy zapisać w postaci
To oznacza, że wykres tej funkcji otrzymamy, znajdując obraz wykresu funkcji w symetrii osiowej względem osi .

Zauważmy, że w ten sposób możemy narysować wykres każdej funkcji , gdzie . Wykres każdej takiej funkcji w całości leży nad osią , więc funkcja nie ma miejsc zerowych. Również każdy z wykresów funkcji przecina oś w punkcie Jednak każda z takich funkcji jest malejąca.
Film dostępny na portalu epodreczniki.pl
Animacja pokazuje wykres funkcji wykładniczej f(x) = 2 do potęgi x i funkcji wykładniczej f(x) = (jedna druga) do potęgi x. Dla różnych argumentów zaznaczone są odpowiadające im wartości funkcji. Zbiorem wartości funkcji wykładniczej f(x) =a do potęgi x, gdzie a jest ustaloną liczbą dodatnią i różną od 1, jest przedział obustronnie otwarty od zera do plus nieskończoności.
Film dostępny na portalu epodreczniki.pl
Animacja pokazuje wykres funkcji wykładniczej f(x) = 2 do potęgi x i funkcji wykładniczej g(x) = (jedna druga) do potęgi x. Dla przeciwnych argumentów zaznaczone są te same wartości funkcji. Opisane funkcje wykładnicze są symetryczne względem osi OY.
Podsumujmy teraz własności funkcji wykładniczych, wykorzystując ich wykresy.
Własności funkcji wykładniczej
Każda funkcja wykładnicza ma następujące własności:
dziedziną jest zbiór wszystkich liczb rzeczywistych,
zbiorem wartości jest przedział ,
asymptotą wykresu funkcji jest prosta o równaniu ,
nie ma miejsc zerowych,
jest monotoniczna, przy czym gdy , to funkcja jest rosnąca, a gdy , to funkcja jest malejąca,
jest różnowartościowa, czyli każdą wartość przyjmuje tylko dla jednego argumentu,
wykres funkcji przecina oś w punkcie .
Omówimy teraz przesunięcia wykresów funkcji wykładniczych wzdłuż osi układu współrzędnych. Jeżeli przesuniemy wykres funkcji wykładniczej o wzdłuż osi , to otrzymamy wykres funkcji o wzorze . Przypomnijmy, że przesunięcie o np. , oznacza przesunięcie wykresu w lewo o jednostki.
Film dostępny na portalu epodreczniki.pl
Animacja przedstawia przesunięcie wykresu funkcji wykładniczej f(x) =2 do potęgi x wzdłuż osi OX układu współrzędnych. W wyniku przesunięcia f(x) o trzy jednostki w prawo otrzymujemy funkcję g(x) =2 do potęgi (x -3). W wyniku przesunięcia f(x) o dwie jednostki w lewo otrzymujemy funkcję h(x) = 2 do potęgi (x +2).
Film dostępny na portalu epodreczniki.pl
Animacja przedstawia przesunięcie wykresu funkcji wykładniczej f(x) =jedna druga do potęgi x wzdłuż osi OX układu współrzędnych. W wyniku przesunięcia f(x) o trzy jednostki w prawo otrzymujemy funkcję g(x) =jedna druga do potęgi (x -3). W wyniku przesunięcia f(x) o dwie jednostki w lewo otrzymujemy funkcję h(x) = jedna druga do potęgi (x +2).
Jeżeli przesuniemy wykres funkcji wykładniczej o wzdłuż osi , to otrzymamy wykres funkcji o wzorze . W tym przypadku przesunięcie o np. oznacza przesunięcie wykresu w dół o jednostki. Asymptotą wykresu funkcji jest teraz prosta o równaniu .
Film dostępny na portalu epodreczniki.pl
Animacja przedstawia przesunięcie wykresu funkcji wykładniczej f(x) =2 do potęgi x wzdłuż osi OY układu współrzędnych. W wyniku przesunięcia f(x) o trzy jednostki w dół otrzymujemy funkcję g(x) =(2 do potęgi x) -3. W wyniku przesunięcia f(x) o dwie jednostki w górę otrzymujemy funkcję h(x) =( 2 do potęgi x) +2.
Film dostępny na portalu epodreczniki.pl
Animacja przedstawia przesunięcie wykresu funkcji wykładniczej f(x) =jedna druga do potęgi x wzdłuż osi OY układu współrzędnych. W wyniku przesunięcia f(x) o trzy jednostki w dół otrzymujemy funkcję g(x) =(jedna druga do potęgi x) -3. W wyniku przesunięcia f(x) o dwie jednostki w górę otrzymujemy funkcję h(x) =( jedna druga do potęgi x) +2.
Przesuniemy wykres funkcji o wzdłuż podanej osi układu współrzędnych.
jeżeli , to wykres przesuwamy o jednostek w górę.
jeżeli , to wykres przesuwamy o jednostek w dół.

Narysujemy otrzymany w ten sposób wykres funkcji oraz zapiszemy jej wzór.
Przesuwając wykres funkcji o wzdłuż osi , otrzymujemy wykres funkcji .
RUM1xxXMTEpvq1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Po przesunięciu wykresu funkcji o wzdłuż osi otrzymujemy wykres funkcji o wzorze.
RdHBTkX7eHcfi1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Po przesunięciu wykresu funkcji wykładniczej o wzdłuż osi otrzymamy wykres funkcji . Ponieważ zbiorem wartości funkcji jest przedział , więc można narysować także prostą o równaniu , która jest asymptotą wykresu funkcji . Rysujemy ją zazwyczaj przerywaną linią.
R1Lg3ZJ1VGsGj1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Przesunięcie o wzdłuż osi oznacza przesunięcie wykresu w dół o jednostki. Wzór funkcji, której wykres otrzymamy po tym przekształceniu, ma postać , a asymptotą jej wykresu jest prosta .
RzDdcOd9vUF3i1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Narysuj wykres funkcji . Podaj wzór funkcji wykładniczej , której wykres przesunęliśmy tak, aby otrzymać wykres funkcji . O ile jednostek i wzdłuż której osi układu współrzędnych wykonaliśmy to przesunięcie? W jakich punktach wykres funkcji przetnie osie i ?
Wykres funkcji to wykres funkcji przesunięty o wzdłuż osi .
R12zrGXhph3431 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Obliczając wartość funkcji dla argumentu , znajdujemy współrzędne punktu przecięcia wykresu funkcji z osią . Mamy
Zatem szukanym punktem jest . Cały wykres leży nad osią , więc nie ma punktów wspólnych z tą osią.
Wzór funkcji możemy zapisać w postaci . Jej wykres powstaje zatem przez przesunięcie wykresu funkcji o wzdłuż osi , czyli o jednostki w lewo.
RxWhhCmsPemWy1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Żeby znaleźć punkt przecięcia wykresu z osią , obliczamy wartość funkcji dla argumentu , czyli
Zatem wykres przecina tę oś w punkcie . Z osią wykres funkcji nie przecina się, ponieważ cały leży nad tą osią.
Wykres funkcji jest wykresem funkcji przesuniętym o wzdłuż osi .
R10zY77X7MAjT1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0., zatem punktem przecięcia wykresu funkcji z osią jest punkt . Cały wykres leży nad osią , zatem nie istnieje punkt przecięcia wykresu z tą osią.
Wykres funkcji powstaje przez przesunięcie wykresu funkcji o wzdłuż osi .
RzHr9oYXlqOHp1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Ponieważ wykres funkcji przecina oś w punkcie , więc punktem przecięcia funkcji z osią jest punkt . Żeby wyznaczyć punkt przecięcia tego wykresu z osią , obliczymy argument, dla którego funkcja przyjmuje wartość , czyli Stąd czyli
Zatem . Punkt przecięcia z osią to punkt .
Film dostępny na portalu epodreczniki.pl
"Animacja przedstawia przesunięcie wykresu funkcji wykładniczej f(x) =2 do potęgi x o wektor [p, q] w układzie współrzędnych. Rozpatrzono przypadki: Dla p>0 oraz q>0 przesunięcie o wektor [3,2] – otrzymano funkcję g(x) =[2 do potęgi (x -3)] +2
Film dostępny na portalu epodreczniki.pl
"Animacja przedstawia przesunięcie wykresu funkcji wykładniczej f(x) =jedna druga do potęgi x o wektor [p, q] w układzie współrzędnych. Rozpatrzono przypadki: Dla p>0 oraz q>0 przesunięcie o wektor [3,2] – otrzymano funkcję g(x) =[jedna druga do potęgi (x -3)] +2
Narysujemy wykres funkcji
Wykres funkcji jest symetryczny względem osi do wykresu funkcji .
R1NKfzYXhM0jF1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Żeby sporządzić wykres funkcji , narysujemy najpierw wykres funkcji . Następnie znajdziemy wykres do niego symetryczny względem osi . Jest to wykres funkcji , który z kolei przesuniemy o wzdłuż osi . W ten sposób otrzymamy wykres funkcji
R1aWQ1voFlJ8c1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Narysujmy wykres funkcji
Przekształćmy wzór funkcji , korzystając z własności potęg
Zatem, żeby narysować wykres funkcji , przesuwamy wykres funkcji o wzdłuż osi .RqrRxaKpcnj5V1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Zapiszmy wzór funkcji w następujący sposób . Zatem rysujemy wykres funkcji , a następnie przesuwamy go o wzdłuż osi .
RrV8Q2Kea7W9g1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Wyznaczymy wzór funkcji wykładniczej , mając dany punkt leżący na jej wykresie.
Skoro punkt leży na wykresie funkcji , więc dla argumentu funkcja przyjmuje wartość . Mamy więc
Po przekształceniu równanie to przyjmuje postać , stąd . Zatem wzór funkcji ma postać .
Sprawdzimy, czy punkt leży na wykresie funkcji .
Wystarczy sprawdzić, czy dla argumentu funkcja przyjmie wartość . Ponieważ , więc punkt leży na wykresie funkcji .
Jaka jest największa, a jaka najmniejsza wartość funkcji wykładniczej w przedziale ?
Funkcja jest rosnąca, ponieważ , a dla funkcja wykładnicza jest rosnąca. Zatem najmniejszą wartość funkcja osiąga dla najmniejszego argumentu z przedziału , czyli dla , a największą dla największego argumentu z tego przedziału, czyli dla . Mamy więc wartość najmniejszą oraz wartość największą w przedziale .
Określ monotoniczność funkcji i na tej podstawie porównaj liczby oraz .
Ponieważ , więc funkcja jest malejąca. Zatem dla mniejszego argumentu przyjmuje wartość większą. Ponieważ , więc .
Wyznaczymy wszystkie argumenty funkcji , dla których wartość funkcji jest
równa
większa od
co najmniej równa
Narysujmy wykres funkcji .

Funkcja wykładnicza jest różnowartościowa, czyli każda wartość jest przyjmowana tylko dla jednego argumentu. Szukamy takiego argumentu , dla którego , czyli . Mamy , stąd .
R1ORUMmXApW1B1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Funkcja jest malejąca, czyli wartości większe od funkcja przyjmuje dla argumentów mniejszych od . Zatem dla .
R1Ub5hsaJBqKw1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Wartości co najmniej równe funkcja przyjmuje dla argumentów mniejszych lub równych . Zatem dla .
Funkcja wykładnicza i jej własności. Przekształcenia wykresu funkcji wykładniczej. Zadania
Dana jest funkcja wykładnicza .
Przeciągnij i upuść.
, , , , , , , , ,
............
............
............
............
............
............
Rozważmy funkcję wykładniczą . Przeciągnij i upuść.
, , ,
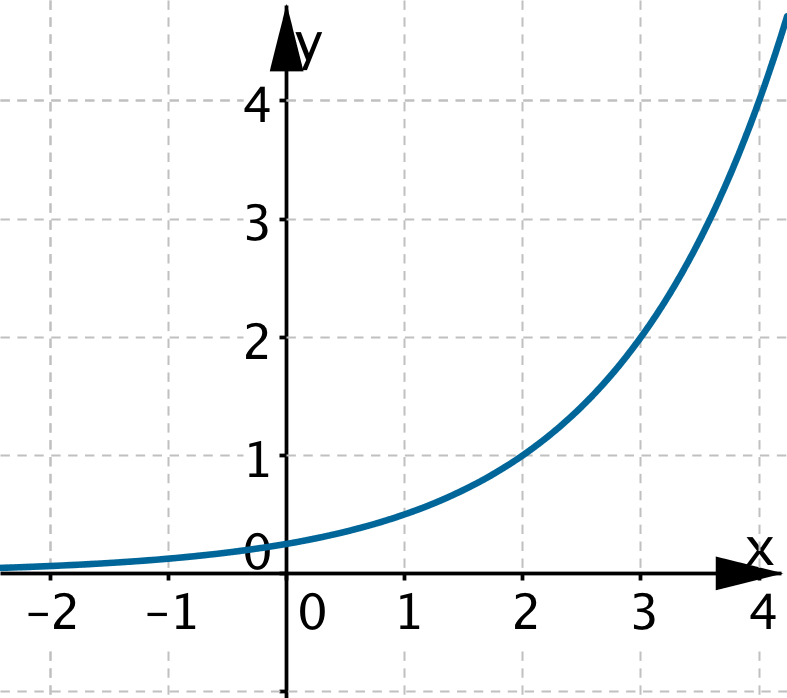
Dopasuj wzór funkcji wykładniczej do wykresu.
, , , , ,
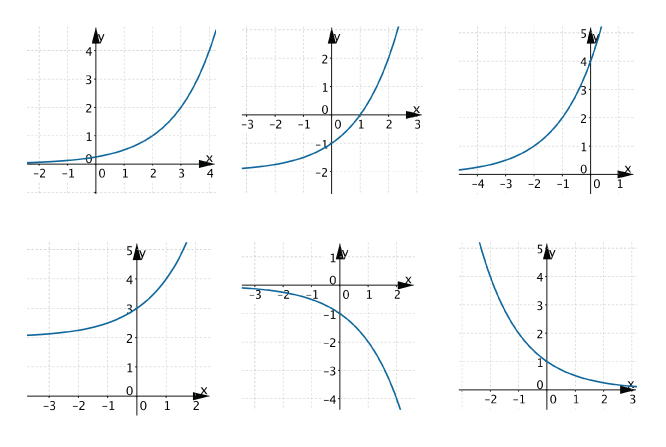
Na wykresie funkcji leży punkt o współrzędnych
Przeciągnij i upuść.
, , , , , , , ,
............
............
............
............
............
............
............
Przeciągnij i upuść.
, , , , , , , ,
............
............
............
............
............
............
............
Punkt leży na wykresie funkcji
Wskaż wzór funkcji rosnącej.
Zbiorem wartości funkcji określonej dla każdego jest przedział
Wyłącznie dodatnie wartości przyjmuje funkcja
Na wykresie funkcji wykładniczej leży punkt . Wówczas
Po przesunięciu wykresu funkcji o wzdłuż osi otrzymamy wykres funkcji określonej wzorem
Wzór funkcji , której wykres jest symetryczny do wykresu funkcji względem osi , ma postać
Funkcja wykładnicza nie przyjmuje wartości
Wykres funkcji przecina oś w punkcie
Znajdź punkt przecięcia wykresu funkcji z osią . Narysuj wykres tej funkcji.
Narysuj wykres funkcji
Narysuj wykres funkcji
Na wykresie funkcji wykładniczej leży punkt . Wyznacz wzór tej funkcji. Określ jej monotoniczność.
Na wykresie funkcji wykładniczej leży punkt . Czy na wykresie tej funkcji leży również punkt ?
Na rysunku przedstawiony jest wykres funkcji wykładniczej oraz zaznaczony jest jeden z punktów leżących na tym wykresie . Wyznacz wzór funkcji .

Wyznacz zbiór wartości funkcji
Połącz wykresy funkcji z ich wzorami
R1RV76kBC7dbb1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.R1HW4dnPyScxm1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.R1K4mDv0uopa51 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.R1WF534mlPNhZ1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.R1ASoMo4vCGmw1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.R14P90Vl7uQYE1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Jaka jest największa, a jaka najmniejsza wartość funkcji w przedziale ?
Wykres której funkcji: , czy przetnie oś w punkcie najdalej leżącym od początku układu współrzędnych?
Dana jest funkcja . Oblicz wartość wyrażenia .
Uporządkuj rosnąco liczby , ,, .
Dla jakiego argumentu funkcja przyjmie wartość ?
Wyznacz wszystkie argumenty, dla których funkcja przyjmuje wartości mniejsze niż funkcja

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DOgeKo121

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DOgeKo121









![Wykres funkcji wykładniczych f(x) =[minus (jedna druga) do potęgi x] +2, g(x) =jedna druga do potęgi x i h(x) = minus (jedna druga) do potęgi x w układzie współrzędnych..](https://static.zpe.gov.pl/portal/f/res-minimized/R1aWQ1voFlJ8c/3/4qCyO2wMOgbqJYoxxh1AoC3Axse4bfuc.svg)








![Wykres funkcji wykładniczych f(x) = [minus (dwie trzecie) do potęgi x] +1, g(x) =dwie trzecie do potęgi x i h(x) = minus (dwie trzecie) do potęgi x w układzie współrzędnych. Wykres funkcji g(x) przekształcamy w symetrii osiowej względem osi OX i otrzymujemy wykres funkcji h(x), który następnie przesuwamy o jeden wzdłuż osi OY. W ten sposób otrzymujemy wykres funkcji f(x). Rozwiązanie zadania podpunkt b.](https://static.zpe.gov.pl/portal/f/res-minimized/Rxz9xsIM9PWPH/3/23pRZuWsnmuDZln9c9wazgYumpANocQL.svg)




![Wykres funkcji rosnącej f(x) = [ 1,6 do potęgi x] +2 leżący pierwszej i drugiej ćwiartce układu współrzędnych. Do wykresu należy punkt o współrzędnych (0, 3).](https://static.zpe.gov.pl/portal/f/res-minimized/R1HW4dnPyScxm/3/2NVkhzsMoFVLb3dwziCU8ruEN7h2QWAA.svg)


![Wykres funkcji malejącej f(x) =[ 0,5 do potęgi x] -2 leżący w drugiej, trzeciej i czwartej ćwiartce układu współrzędnych. Do wykresu należą punkty o współrzędnych (-1, 0) i (0, -1).](https://static.zpe.gov.pl/portal/f/res-minimized/R1ASoMo4vCGmw/3/2GJTVmcOEnD1O9GcCgcLMxpJ4wwmWTCd.svg)

