Ciąg arytmetyczny
Ciąg arytmetyczny

Film dostępny na portalu epodreczniki.pl
Animacja pokazuje chłopca uczącego się języka angielskiego. Pierwszego dnia nauki powtórzył wszystkie znane mu słowa, które znał i okazało się, że łącznie pamięta 370 słów. Postanowił, że każdego następnego dnia nauczy się 12 nowych słów. Ile słów Tomek będzie znał po 3 dniach, a ile po 15 dniach nauki? Po pierwszym dniu nauki Tomek znał 370 słów. Po drugim dniu będzie znał 370 +12= 382 słowa, po trzecim 370 +12 +12 =370 +2 razy 12 =394 słowa, po czwartym 370 +3 razy 12 =406 słów, i tak dalej. Jeżeli przez (a z indeksem dolnym n) oznaczymy liczbę słów, które Tomek będzie znał po n dniach nauki, to otrzymujemy: a z indeksem dolnym jeden =370, a z indeksem dolnym dwa =382, a z indeksem dolnym trzy =394, a z indeksem dolnym cztery =406, … . Zastanówmy się, ile słów będzie znał Tomek po 15 dniach nauki. Każdego dnia (poza pierwszym) Tomek poznaje 12 nowych słów, więc przez 14 dni (od drugiego do piętnastego włącznie) pozna 14 razy 12 nowych słów, a więc po 15 dniach nauki będzie znał a z indeksem dolnym piętnaście =370 +14 razy12 =538 słów. W ogólnym przypadku, po n dniach nauki Tomek będzie znał (a z indeksem dolnym n) =370 +(n?1) razy12 słów. Otrzymaliśmy ciąg, w którym pierwszy wyraz jest równy 370, a każdy następny wyraz jest większy od poprzedniego o 12. Zatem ciąg ten możemy opisać za pomocą dwóch równości: a z indeksem dolnym jeden =370 i a z indeksem dolnym n +1 = a z indeksem dolnym n +12 dla n większe lub równe 1. Rozpatrywany przez nas ciąg, to przykład ciągu arytmetycznego.
Ciąg nazywamy arytmetycznym, jeżeli ma co najmniej wyrazy i każdy jego wyraz, począwszy od drugiego, jest sumą wyrazu poprzedniego i pewnej ustalonej liczby. Liczbę tę nazywamy różnicą ciągu i oznaczamy ją .
Jeśli więc ciąg jest skończony i ma wyrazów, to dla dowolnej liczby całkowitej . Jeśli natomiast ciąg jest nieskończony, to dla dowolnej liczby całkowitej .

Film dostępny na portalu epodreczniki.pl
Animacja prezentuje trzy wykresy ciągu arytmetycznego w układach współrzędnych. Przykład 1. Dany jest pierwszy wyraz ciągu a z indeksem dolnym jeden =3, kolejny wyraz ciągu a z indeksem dolnym n +1 = (a z indeksem dolnym n) +r, gdzie r różnica ciągu arytmetycznego. Dla r =2 otrzymano kolejne wyrazy ciągu a z indeksem dolnym dwa =5, a z indeksem dolnym trzy = 7, a z indeksem dolnym cztery =9. Jeżeli r>0, to punkty będące wyrazami ciągu leżą na prostej, która ilustruje funkcję rosnącą. Przykład 2. Dany jest pierwszy wyraz ciągu a z indeksem dolnym jeden =2, kolejny wyraz ciągu a z indeksem dolnym n +1 = (a z indeksem dolnym n) +r, gdzie r różnica ciągu arytmetycznego. Dla r =0 otrzymano kolejne wyrazy ciągu a z indeksem dolnym dwa =2, a z indeksem dolnym trzy =2, a z indeksem dolnym cztery =2. Jeżeli r =0, to punkty będące wyrazami ciągu leżą na prostej, która ilustruje funkcję stałą. Przykład 3. Dany jest pierwszy wyraz ciągu a z indeksem dolnym jeden =1, kolejny wyraz ciągu a z indeksem dolnym n +1 = (a z indeksem dolnym n) +r, gdzie r różnica ciągu arytmetycznego. Dla r =-1,5 otrzymano kolejne wyrazy ciągu a z indeksem dolnym dwa =-0,5, a z indeksem dolnym trzy =-2, a z indeksem dolnym cztery =-3,5. Jeżeli r
Zauważmy, że jeżeli znamy , czyli pierwszy wyraz ciągu arytmetycznego, oraz różnicę tego ciągu, to możemy wyznaczyć dowolny wyraz tego ciągu.
Wystarczy zatem do wyrazu dodać razy różnicę tego ciągu. Otrzymaliśmy w ten sposób wzór na -ty wyraz ciągu arytmetycznego.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DyliBdW4j
Każdy wyraz ciągu arytmetycznego o różnicy jest równy .
Zależność między dwoma kolejnymi wyrazami ciągu arytmetycznego, a więc równość możemy też zapisać w postaci równoważnej

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DyliBdW4j

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DyliBdW4j
Sprawdź, czy nieskończony ciąg określony wzorem ogólnym jest ciągiem arytmetycznym. Jeżeli tak, to oblicz jego różnicę.
Zbadamy różnicę dwóch kolejnych wyrazów ciągu . Wyznaczmy najpierw
Wtedy
Otrzymana różnica jest stała (nie zależy od ), co oznacza, że rozważany ciąg jest arytmetyczny, a otrzymana liczba to właśnie różnica tego ciągu.
Zauważmy, że
Wzór na -ty wyraz to , co jest zgodne z tym, że .
Pierwszy wyraz ciągu arytmetycznego jest równy , a różnica tego ciągu jest równa . Oblicz dziesiąty oraz trzydziesty drugi wyraz tego ciągu.
Korzystając ze wzoru na -ty wyraz ciągu arytmetycznego, mamy
Piąty wyraz pewnego ciągu arytmetycznego jest równy , a siódmy wyraz tego ciągu jest równy . Podaj wyraz jedenasty tego ciągu.
Obliczymy jedenasty wyraz ciągu dwoma sposobami.
sposób
Zapiszemy, korzystając ze wzoru na -ty wyraz ciągu arytmetycznego, wyrazy i
oraz
Otrzymujemy układ równań z dwiema niewiadomymi i
Rozwiążmy ten układ:
Możemy teraz, ponownie stosując wzór na -ty wyraz ciągu arytmetycznego, obliczyć wyraz jedenasty
sposób
Zauważmy, że wyraz siódmy różni się od piątego wyrazu o , gdyż oraz . Zatem . Szukany wyraz jedenasty różni się od wyrazu siódmego o . Zatem
Zwróćmy uwagę, że każdy ciąg arytmetyczny jest monotoniczny.
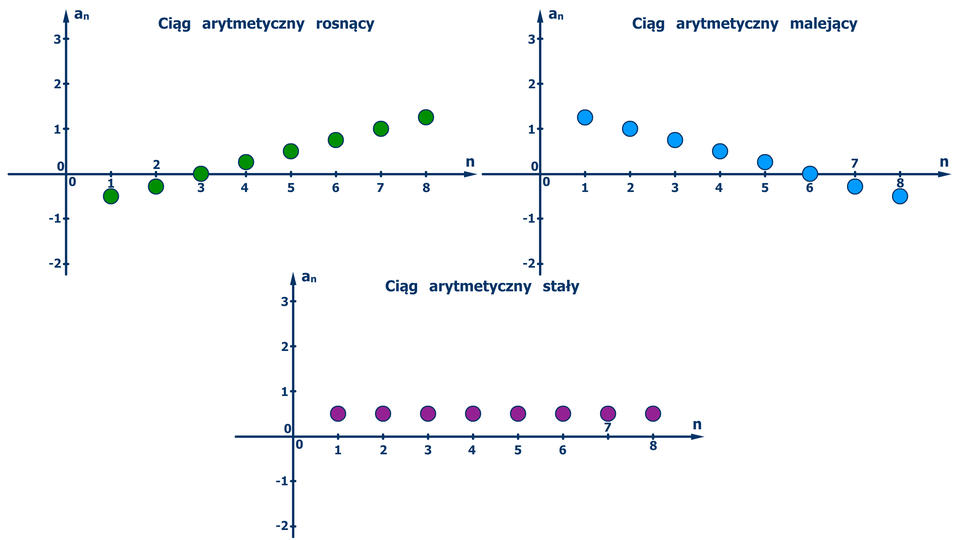
Film dostępny na portalu epodreczniki.pl
Animacja
Jeżeli różnica ciągu arytmetycznego jest dodatnia, to ciąg ten jest rosnący. Jeżeli różnica ciągu arytmetycznego jest ujemna, to ciąg ten jest malejący. Jeżeli różnica ciągu arytmetycznego jest równa zero, to ciąg jest stały i jego wszystkie wyrazy są równe .

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DyliBdW4j
Zauważmy, że każdy punkt wykresu ciągu arytmetycznego leży na prostej o równaniu , czyli , gdzie oraz (różnica i pierwszy wyraz ciągu) to ustalone dla danego ciągu liczby. Współczynnik kierunkowy tej prostej jest równy różnicy ciągu. Tak więc ciąg jest:
rosnący, gdy rosnąca jest funkcja liniowa, której wykresem jest ta prosta, a więc gdy współczynnik kierunkowy tej prostej jest dodatni, czyli ;
malejący, gdy malejąca jest funkcja liniowa, której wykresem jest ta prosta, a więc gdy współczynnik kierunkowy tej prostej jest ujemny, czyli ;
stały, gdy stała jest funkcja liniowa, której wykresem jest ta prosta, a więc gdy współczynnik kierunkowy tej prostej jest równy zero, czyli .
Ciąg jest arytmetyczny oraz i . Oblicz pierwszy wyraz oraz różnicę ciągu .
Ze wzoru na -ty wyraz ciągu arytmetycznego możemy zapisać wyrazy , i w zależności od i . Możemy wtedy zapisać równanie podane w treści zadania, w postaci . Stąd . Podobnie możemy zapisać równanie w postaci . W ten sposób otrzymujemy równanie z jedną niewiadomą
Przekształcamy je w sposób równoważny
Obliczamy wyróżnik tego równania . Zatem równanie to ma dwa rozwiązania oraz .
To oznacza, że istnieją dwa ciągi arytmetyczne, których wyrazy spełniają podane w treści zadania warunki. Gdy , to , a gdy , to .
Połącz w pary wzór ogólny ciągu arytmetycznego z odpowiednimi wartościami i .
<span aria-label="a indeks dolny, jeden, równa się, początek ułamka, jeden, mianownik, dwa, koniec ułamka, przecinek, r, równa się, minus, pięć" role="math"><math><msub><mi>a</mi><mn>1</mn></msub><mo> </mo><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>,</mo><mo> </mo><mo> </mo><mo> </mo><mi>r</mi><mo>=</mo><mo>-</mo><mn>5</mn></math></span>, <span aria-label="a indeks dolny, jeden, równa się, minus, pięć, przecinek, r, równa się, początek ułamka, jeden, mianownik, dwa, koniec ułamka" role="math"><math><msub><mi>a</mi><mn>1</mn></msub><mo> </mo><mo>=</mo><mo>-</mo><mn>5</mn><mo>,</mo><mo> </mo><mo> </mo><mo> </mo><mi>r</mi><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac></math></span>, <span aria-label="a indeks dolny, jeden, równa się, pięć, przecinek, r, równa się, początek ułamka, jeden, mianownik, dwa, koniec ułamka" role="math"><math><msub><mi>a</mi><mn>1</mn></msub><mo> </mo><mo>=</mo><mn>5</mn><mo>,</mo><mo> </mo><mo> </mo><mo> </mo><mi>r</mi><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac></math></span>, <span aria-label="a indeks dolny, jeden, równa się, początek ułamka, jeden, mianownik, dwa, koniec ułamka, przecinek, r, równa się, pięć" role="math"><math><msub><mi>a</mi><mn>1</mn></msub><mo> </mo><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>,</mo><mo> </mo><mo> </mo><mo> </mo><mi>r</mi><mo>=</mo><mn>5</mn></math></span>, <span aria-label="a indeks dolny, jeden, równa się, pięć, przecinek, r, równa się, minus, początek ułamka, jeden, mianownik, dwa, koniec ułamka" role="math"><math><msub><mi>a</mi><mn>1</mn></msub><mo> </mo><mo>=</mo><mn>5</mn><mo>,</mo><mo> </mo><mo> </mo><mo> </mo><mi>r</mi><mo>=</mo><mo>-</mo><mfrac><mn>1</mn><mn>2</mn></mfrac></math></span>, <span aria-label="a indeks dolny, jeden, równa się, minus, pięć, przecinek, r, równa się, minus, początek ułamka, jeden, mianownik, dwa, koniec ułamka" role="math"><math><msub><mi>a</mi><mn>1</mn></msub><mo> </mo><mo>=</mo><mo>-</mo><mn>5</mn><mo>,</mo><mo> </mo><mo> </mo><mo> </mo><mi>r</mi><mo>=</mo><mo>-</mo><mfrac><mn>1</mn><mn>2</mn></mfrac></math></span>
Uporządkuj tak, aby uzyskać malejący ciąg arytmetyczny.
Wyrazami nieskończonego ciągu są kolejne liczby naturalne, które przy dzieleniu przez dają resztę , a trzeci wyraz tego ciągu . Oblicz siedemdziesiąty wyraz tego ciągu.
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.
- Ciąg jest ciągiem arytmetycznym.
- Ciąg jest ciągiem arytmetycznym o różnicy .
- Ciąg jest ciągiem arytmetycznym rosnącym.
Liczby w podanej kolejności tworzą ciąg arytmetyczny. Wyznacz i .
Pomiędzy liczby i wstaw siedem liczb, tak aby razem z liczbami i tworzyły ciąg arytmetyczny.
Dany jest ciąg arytmetyczny , w którym oraz . Wyznacz równanie prostej, w której zawarty jest wykres ciągu .
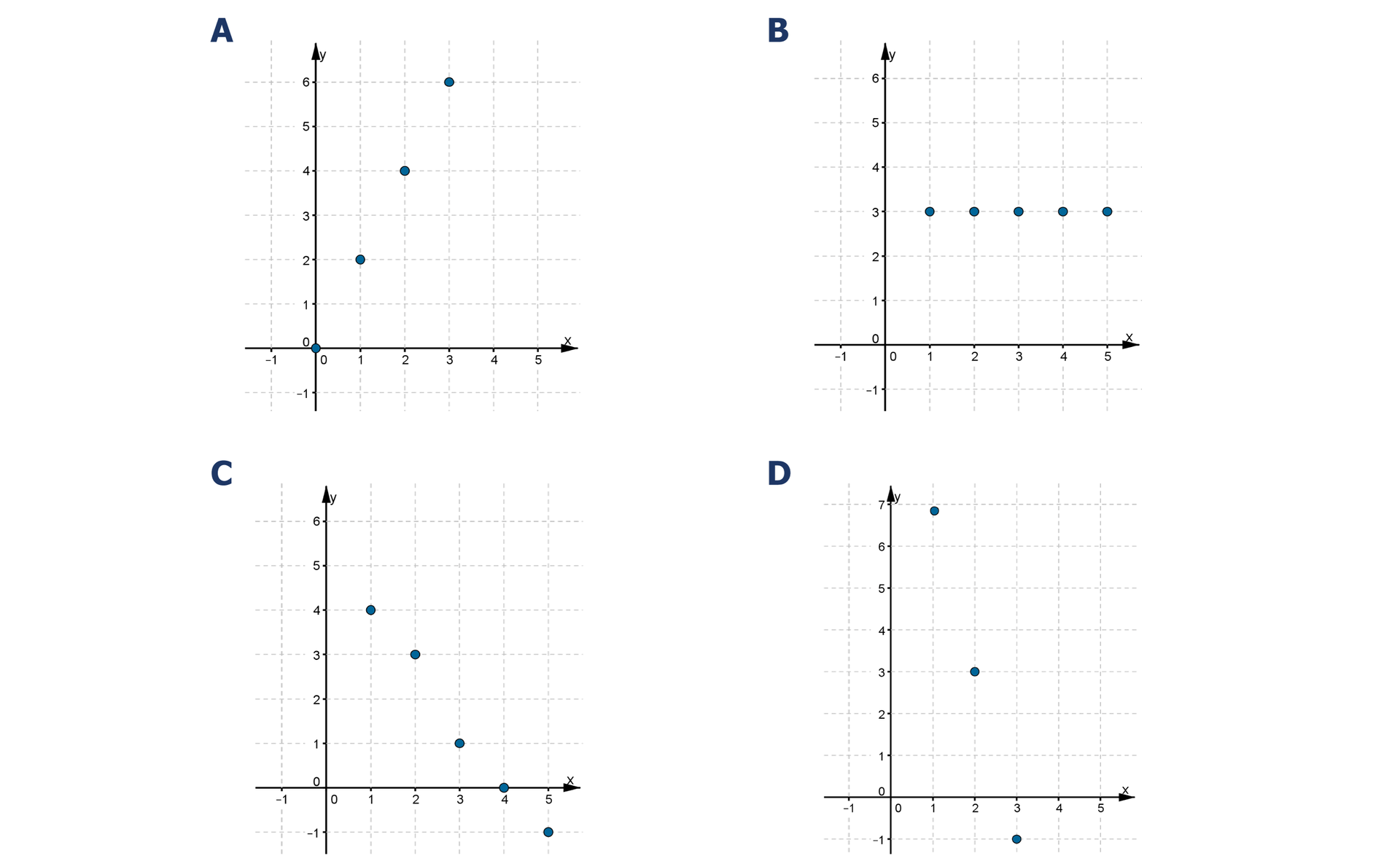
Który z rysunków przedstawia wykres ciągu arytmetycznego?
Wyrazy każdego nieskończonego ciągu arytmetycznego spełniają warunek
Liczby są trzema początkowymi wyrazami ciągu arytmetycznego określonego dla . Wzór ogólny tego ciągu ma postać.
Dany jest ciąg arytmetyczny , w którym i . Wtedy pierwszy wyraz ciągu jest równy
Ciąg arytmetyczny jest określony wzorem . Wtedy
Ciąg arytmetyczny jest określony wzorem . Ile wyrazów tego ciągu jest dodatnich?
Sprawdź, czy podany ciąg jest arytmetyczny. Jeżeli tak, to podaj jego różnicę.
Połącz w pary ciąg arytmetyczny z odpowiadającą mu różnicą.
<span aria-label="nawias, dwa początek ułamka, jeden, mianownik, trzy, koniec ułamka, przecinek, cztery początek ułamka, jeden, mianownik, trzy, koniec ułamka, przecinek, sześć początek ułamka, jeden, mianownik, trzy, koniec ułamka, przecinek, osiem początek ułamka, jeden, mianownik, trzy, koniec ułamka, przecinek, wielokropek, zamknięcie nawiasu" role="math"><math><mfenced><mrow><mn>2</mn><mfrac><mn>1</mn><mn>3</mn></mfrac><mo>,</mo><mn>4</mn><mfrac><mn>1</mn><mn>3</mn></mfrac><mo>,</mo><mn>6</mn><mfrac><mn>1</mn><mn>3</mn></mfrac><mo>,</mo><mn>8</mn><mfrac><mn>1</mn><mn>3</mn></mfrac><mo>,</mo><mo>…</mo></mrow></mfenced></math></span>, <span aria-label="nawias, pięć początek ułamka, jeden, mianownik, sześć, koniec ułamka, przecinek, cztery początek ułamka, pięć, mianownik, sześć, koniec ułamka, przecinek, cztery początek ułamka, jeden, mianownik, dwa, koniec ułamka, przecinek, cztery początek ułamka, jeden, mianownik, sześć, koniec ułamka, przecinek, wielokropek, zamknięcie nawiasu" role="math"><math><mfenced><mrow><mn>5</mn><mfrac><mn>1</mn><mn>6</mn></mfrac><mo>,</mo><mn>4</mn><mfrac><mn>5</mn><mn>6</mn></mfrac><mo>,</mo><mn>4</mn><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>,</mo><mn>4</mn><mfrac><mn>1</mn><mn>6</mn></mfrac><mo>,</mo><mo>…</mo></mrow></mfenced></math></span>, <span aria-label="nawias, trzy początek ułamka, jeden, mianownik, trzy, koniec ułamka, przecinek, trzy początek ułamka, pięć, mianownik, sześć, koniec ułamka, przecinek, cztery początek ułamka, jeden, mianownik, trzy, koniec ułamka, przecinek, cztery początek ułamka, pięć, mianownik, sześć, koniec ułamka, przecinek, wielokropek, zamknięcie nawiasu" role="math"><math><mfenced><mrow><mn>3</mn><mfrac><mn>1</mn><mn>3</mn></mfrac><mo>,</mo><mn>3</mn><mfrac><mn>5</mn><mn>6</mn></mfrac><mo>,</mo><mn>4</mn><mfrac><mn>1</mn><mn>3</mn></mfrac><mo>,</mo><mn>4</mn><mfrac><mn>5</mn><mn>6</mn></mfrac><mo>,</mo><mo>…</mo></mrow></mfenced></math></span>, <span aria-label="nawias, cztery początek ułamka, jeden, mianownik, dwa, koniec ułamka, przecinek, cztery początek ułamka, pięć, mianownik, sześć, koniec ułamka, przecinek, pięć początek ułamka, jeden, mianownik, sześć, koniec ułamka, przecinek, pięć początek ułamka, jeden, mianownik, dwa, koniec ułamka, przecinek, wielokropek, zamknięcie nawiasu" role="math"><math><mfenced><mrow><mn>4</mn><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>,</mo><mn>4</mn><mfrac><mn>5</mn><mn>6</mn></mfrac><mo>,</mo><mn>5</mn><mfrac><mn>1</mn><mn>6</mn></mfrac><mo>,</mo><mn>5</mn><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>,</mo><mo>…</mo></mrow></mfenced></math></span>, <span aria-label="nawias, pięć początek ułamka, jeden, mianownik, dwa, koniec ułamka, przecinek, trzy początek ułamka, jeden, mianownik, dwa, koniec ułamka, przecinek, jeden początek ułamka, jeden, mianownik, dwa, koniec ułamka, przecinek, minus, początek ułamka, jeden, mianownik, dwa, koniec ułamka, przecinek, wielokropek, zamknięcie nawiasu" role="math"><math><mfenced><mrow><mn>5</mn><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>,</mo><mn>3</mn><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>,</mo><mn>1</mn><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>,</mo><mo>-</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>,</mo><mo>…</mo></mrow></mfenced></math></span>, <span aria-label="nawias, trzy początek ułamka, jeden, mianownik, dwa, koniec ułamka, przecinek, trzy kropka dwa początek ułamka, jeden, mianownik, dwa, koniec ułamka, przecinek, dwa, przecinek, wielokropek, zamknięcie nawiasu" role="math"><math><mfenced><mrow><mn>3</mn><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>,</mo><mn>3</mn><mo>,</mo><mn>2</mn><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>,</mo><mn>2</mn><mo>,</mo><mo>…</mo></mrow></mfenced></math></span>
| 2 | |
| -2 | |
Wyznacz wzór ogólny ciągu arytmetycznego, wiedząc, że oraz .
Oblicz pierwszy wyraz ciągu arytmetycznego , którego różnica jest równa oraz ósmy wyraz jest równy .
Wyznacz takie liczby i , żeby ciąg był arytmetyczny.
Oblicz pierwszy wyraz i różnicę malejącego ciągu arytmetycznego , w którym oraz .
Ciąg arytmetyczny składa się z trzechwyrazów. Ich suma jest równa , a suma ich kwadratów jest równa Oblicz wyrazy tego ciągu.
Miary kątów w pewnym czworokącie tworzą ciąg arytmetyczny. Największy z kątów ma miarę . Oblicz miary pozostałych kątów tego czworokąta.
Rozważmy ciąg trójkątów równobocznych, których długości boków tworzą ciąg arytmetyczny.
Czy obwody tych trójkątów tworzą ciąg arytmetyczny?
Czy pola tych trójkątów tworzą ciąg arytmetyczny?
Wykaż, że jeżeli cyfry liczby trzycyfrowej tworzą ciąg arytmetyczny, to liczba ta jest podzielna przez
Oblicz, ile wyrazów ma ciąg arytmetyczny, w którym suma dwóch pierwszych wyrazów jest równa , suma dwóch ostatnich wyrazów jest równa , a wyraz jedenasty jest równy
Wykaż, że jeżeli w ciągu arytmetycznym prawdziwe są zależności oraz dla , to różnica tego ciągu jest równa

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DyliBdW4j