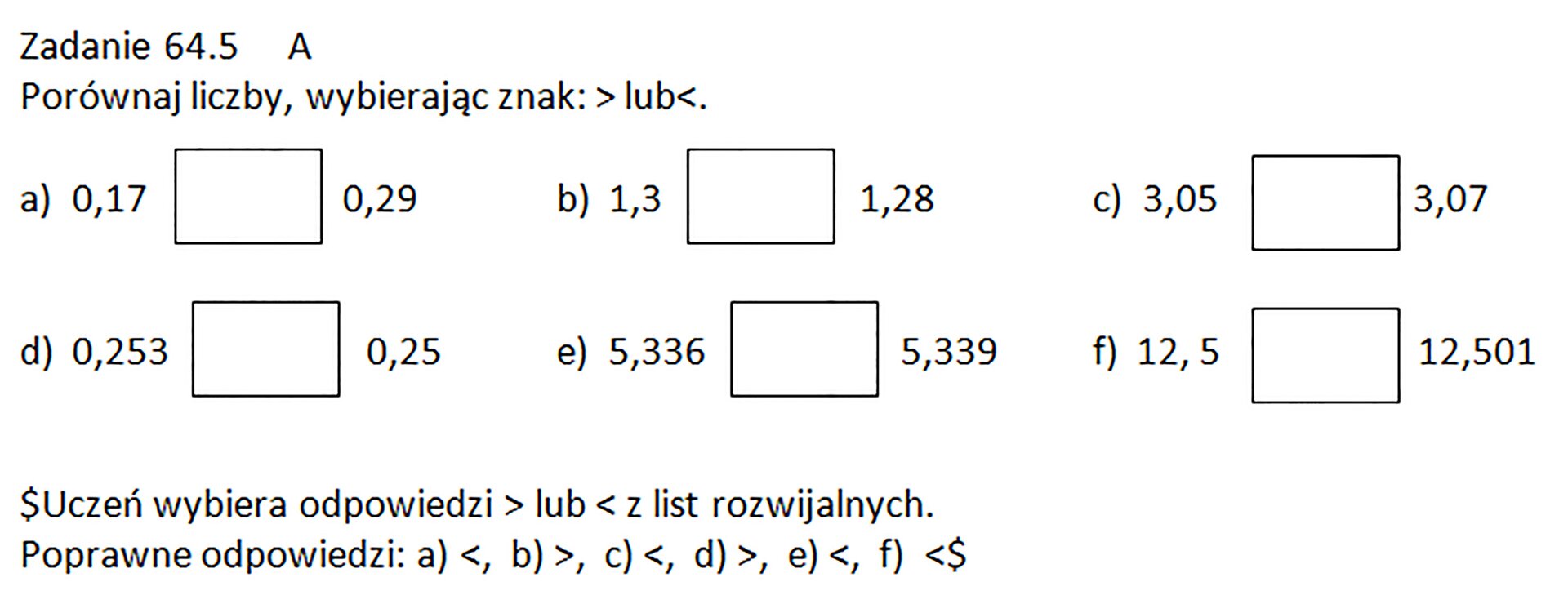Porównywanie liczb dziesiętnych
Wśród podanych liczb znajdują się cztery, które są sobie równe. Czy domyślasz się, które to liczby?
Aby przekonać się, że wybrane liczby są równe, zamienimy wszystkie dane liczby na ułamki zwykłe, a następnie niektóre z nich skrócimy.
Widzimy, że
Zapis tych czterech liczb różni się tylko zerami na końcu części dziesiętnych. Okazuje się, że w liczbie dziesiętnej możemy na końcu dopisywać lub opuszczać zera, a liczba się nie zmieni.
Opuszczanie końcowych zer, to skracanie liczb dziesiętnych przez … itd.
. Liczbę skróciliśmy przez
. Liczbę skróciliśmy przezDopisywanie końcowych zer w liczbach dziesiętnych , to ich rozszerzanie przez … itd.
. Liczbę rozszerzyliśmy przez
Rozszerz podane liczby
1,2000, 0,024000, 1,20, 4,3210, 0,02400, 0,0500, 10,03000, 10,0300, 1,50, 0,00600, 0,0060, 0,600, 0,60, 0,050, 4,32100, 1,500
a) przez 10.
0,6 = ................ 1,2 = ................
0,05 = ................ 4,321 = ................
b) przez 100.
1,5 = ................ 0,024 = ................
10,03 = ................ 0,006 = ................
Podane liczby skróć przez .
Połącz w pary.
0,011, 0,01, 0,1, 0,11, 0,001
| 0,10 | |
| 0,0100 | |
| 0,0110 | |
| 0,11000 | |
| 0,0010 |
Film dostępny na portalu epodreczniki.pl
Animacja
Porównaj liczby i wybierz.
różną liczbę, >, >, większą liczbę, większą liczbę, różną liczbę, <, <, >, <
a) 5,07 .................................. 8,07
b) 6,3 .................................. 2,99
c) 20,001 .................................. 10,087
Jeżeli liczby dziesiętne mają .................................. całości, to ta z nich jest większa, która ma .................................. całości.
Liczby: ustawimy w kolejności malejącej, to znaczy od największej do najmniejszej.
Aby porównać te liczby, do dwóch z nich dopiszemy na końcu zera, rozszerzając je przez . Potem zamienimy je na ułamki zwykłe.
Wszystkie ułamki mają ten sam mianownik, zatem
Wobec tego
Jeżeli liczby mają tyle samo całości, to ta jest większa, która ma więcej części dziesiątych.
Jeżeli liczby mają tyle samo całości i tyle samo części dziesiątych, to ta jest większa, która ma więcej części setnych.
Analogiczna zasada dotyczy kolejnych części dziesiętnych.
Porównaj liczby i wybierz.
<, <, >, <, >, >, <, >, >, >, <, <
a) 0,17 ............ 0,29
b) 1,3 ............ 1,28
c) 3,05 ............ 3,07
d) 0,253 ............ 0,25
e) 5,336 ............ 5,339
f) 12,5 ............ 12,501
Uporządkuj w kolejności malejącej.
-
długopis
3,26 zł -
ekierka
2,59 zł -
zeszyt
3,15 zł -
temperówka
2,04 zł -
cyrkiel
4,05 zł

Film dostępny na portalu epodreczniki.pl
Animacja
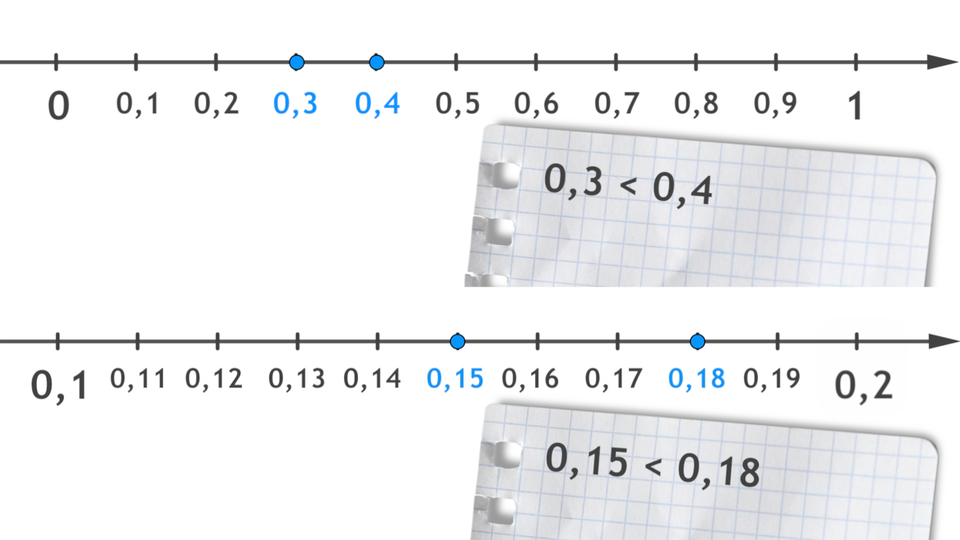
Zasadę powiększania można stosować do kolejnych fragmentów osi zamieszczonych wcześniej.
Na osiach liczbowych zaznaczono punkty , . Określ współrzędne tych punktów.
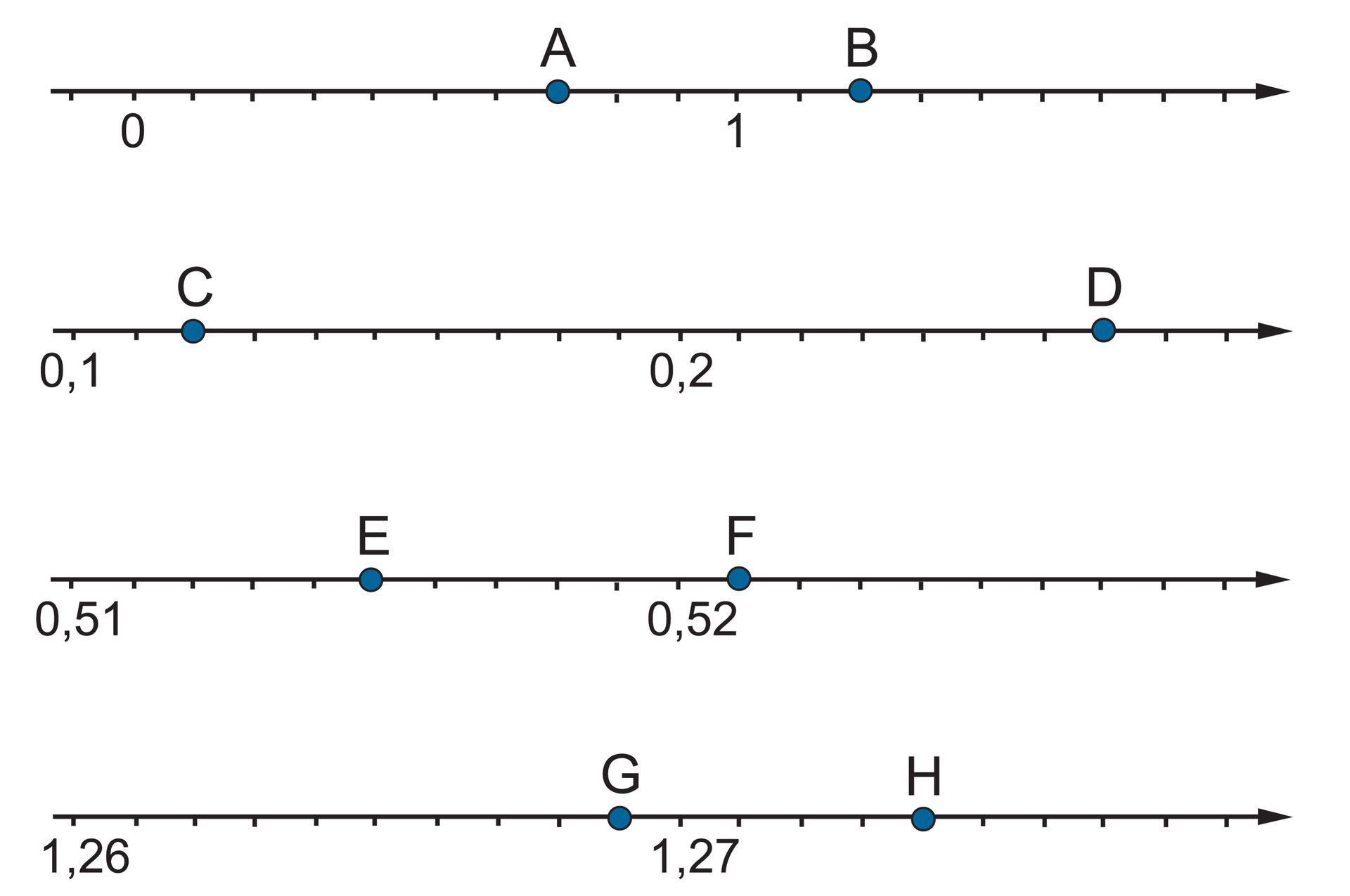
Liczby, które są współrzędnymi punktów zapisz w kolejności rosnącej.