Przeczytaj

Omówimy przesunięcie paraboli, będącej wykresem funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej $f$ określonej wzorem $f (x) = a x^{2}$ , gdzie $a \in ℝ ∖ \{0\}$ , wzdłuż osi $X$ i osi $Y$ układu współrzędnych.

o przesunięciu wykresu funkcji wzdłuż osi

X

i osi

Y

Twierdzenie: o przesunięciu wykresu funkcji wzdłuż osi

X

i osi

Y

Wykres funkcji $f (x - p) + q$ otrzymujemy w wyniku przesunięcia wykresu funkcji $f$ wzdłuż osi $X$ o $p$ jednostek w prawo, gdy $p > 0$ lub o $p$ jednostek w lewo, gdy $p < 0$ oraz wzdłuż osi $Y$ o $q$ jednostek w górę, gdy $q > 0$ lub o $q$ jednostek w dół, gdy $q < 0$ .

Naszkicujmy wykres funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej $f$ określonej wzorem $f (x) = 2 x^{2}$ .

W celu naszkicowania wykresu przedstawmy w tabeli wartości funkcji $f$ dla kilku argumentów:

Argumenty i wartości funkcji $f$
$x$	$- 2$	$- 1$	$0$	$1$	$2$
$f (x)$	$8$	$2$	$0$	$2$	$8$

Wykres funkcji $f$ przedstawia się następująco:

RZAsfG9RCvqrx

Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus pięciu do pięciu, oraz z pionową osią Y od minus jeden do pięciu. Na płaszczyźnie, niebieskim kolorem narysowano wykres funkcji fx. Wykresem funkcji jest parabola o wierzchołku w punkcie 0;0 i ramionach skierowanych w górę. Wykres funkcji przebiega przez punkty o współrzędnych -1;2, oraz 1;2.

Wykres funkcji $f$ przesuniemy o $2$ jednostki w prawo wzdłuż osi $X$ i o $1$ jednostkę w górę wzdłuż osi $Y$ .

W wyniku tego przekształceniaprzekształcenie wykresu funkcji $f (x - p) + q$ przekształcenia otrzymujemy wykres funkcji $g$ określonej wzorem $g (x) = f (x - 2) + 1$ .

Wykresy funkcji $f$ i $g$ przedstawiają się następująco:

R1GtzpK02TLiw

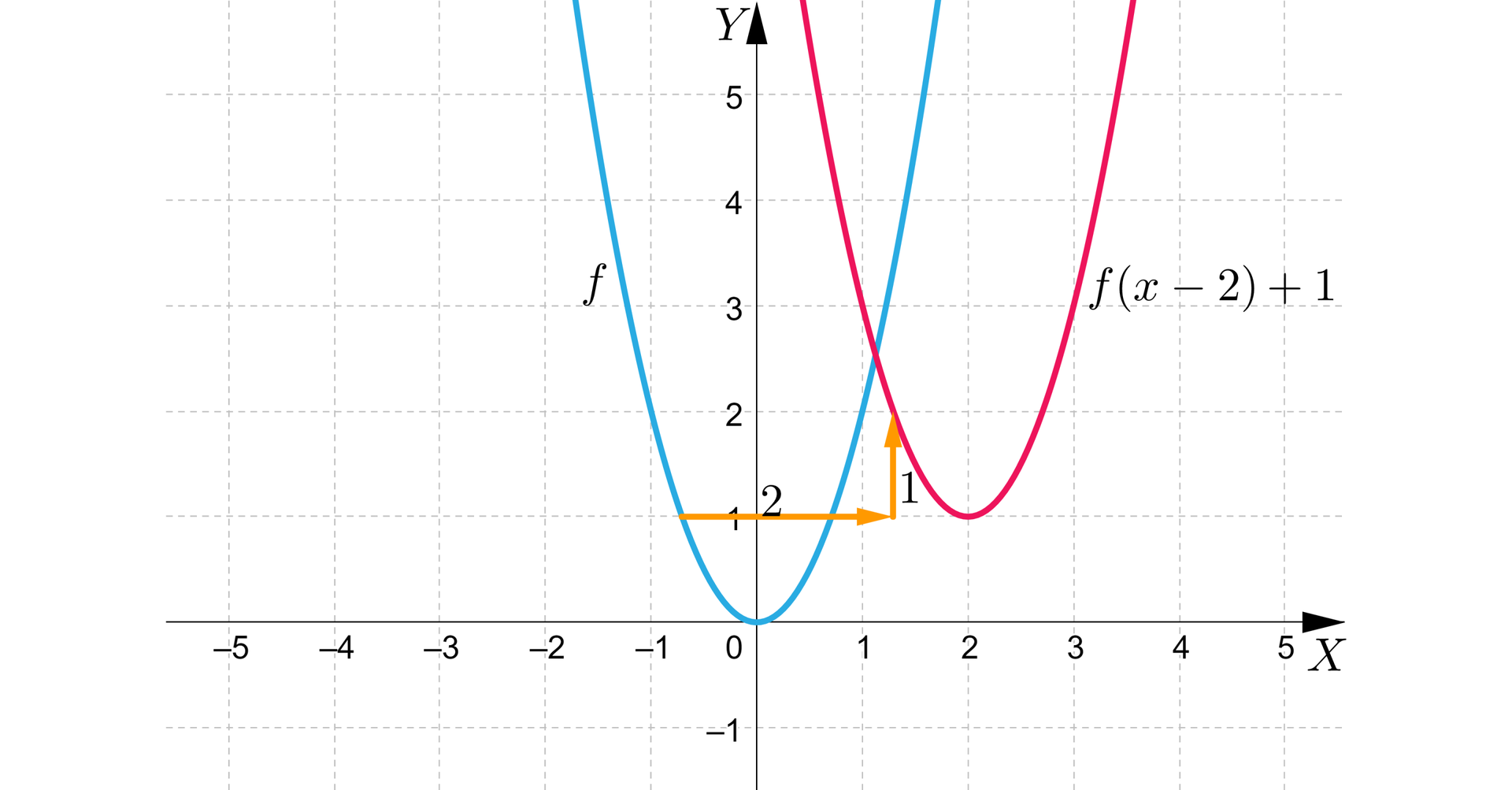
Zauważmy, że przy przesunięciu wykresu funkcji $f$ o $2$ jednostki w prawo wzdłuż osi $X$ i $1$ jednostkę w górę wzdłuż osi $Y$ otrzymujemy wykres funkcji $g$ o następujących własnościach:

zbiór wartości funkcji: $y \in ⟨1, \infty)$
współrzędne wierzchołka paraboli, będącej wykresem funkcji $g$ : $(2, 1)$ ,
równanie osi symetrii paraboli, będącej wykresem funkcji $g$ : $x = 2$ ,
funkcja $g$ jest malejąca w przedziale $(- \infty, 2⟩$ ,
funkcja $g$ jest rosnąca w przedziale $⟨2, \infty)$ ,
wartość najmniejsza funkcji $g$ wynosi $1$ dla $x = 2$ .

Jeżeli przesuwamy parabolę, będącą wykresem funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej $f$ określonej wzorem $f (x) = a x^{2}$ , gdzie $a > 0$ , wzdłuż osi $X$ o $p$ jednostek w prawo lub o $p$ jednostek w lewo oraz wzdłuż osi $Y$ o $q$ jednostek w górę lub o $q$ jednostek w dół, to otrzymujemy parabolę, będącą wykresem funkcji $g$ o następujących własnościach:

zbiór wartości funkcji: $y \in ⟨q, \infty)$
współrzędne wierzchołka paraboli, będącej wykresem funkcji $g$ : $(p, q)$ ,
równanie osi symetrii paraboli, będącej wykresem funkcji $g$ : $x = p$ ,
funkcja $g$ jest malejąca w przedziale $(- \infty, p⟩$ ,
funkcja $g$ jest rosnąca w przedziale $⟨p, \infty)$ ,
wartość najmniejsza funkcji $g$ wynosi $q$ dla $x = p$ .

Sporządźmy wykres funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej $f$ określonej wzorem $f (x) = - 2 x^{2}$ .

W celu naszkicowania wykresu przedstawmy w tabeli wartości funkcji $f$ dla kilku argumentów:

Argumenty i wartości funkcji $f$
$x$	$- 2$	$- 1$	$0$	$1$	$2$
$f (x)$	$- 8$	$- 2$	$0$	$- 2$	$- 8$

Wykres funkcji $f$ przedstawia się następująco:

R1KO5CVYtZrRu

Ilustracja przedstawia poziomą oś X od minus pięciu do pięciu oraz pionowa oś Y od minus pięciu do jedynki. Na rysunku zaznaczono także wykres funkcji kwadratowe f będącej parabolą z wierzchołkiem w punkcie nawias zero średnik zero oraz z ramionami skierowanymi w dół. Parabola przechodzi przez punkty nawias minus jeden średnik minus dwa koniec nawiasu oraz jeden średnik minus dwa koniec nawiasu.

Wykres funkcji $f$ przesuniemy o $3$ jednostki w lewo wzdłuż osi $X$ i o $2$ jednostki w górę wzdłuż osi $Y$ .

W wyniku tego przekształceniaprzekształcenie wykresu funkcji $f (x - p) + q$ przekształcenia otrzymujemy wykres funkcji $g$ określonej wzorem $g (x) = f (x + 3) + 2$ .

Wykresy funkcji $f$ i $g$ przedstawiają się następująco:

R1APEJTBSBqqy

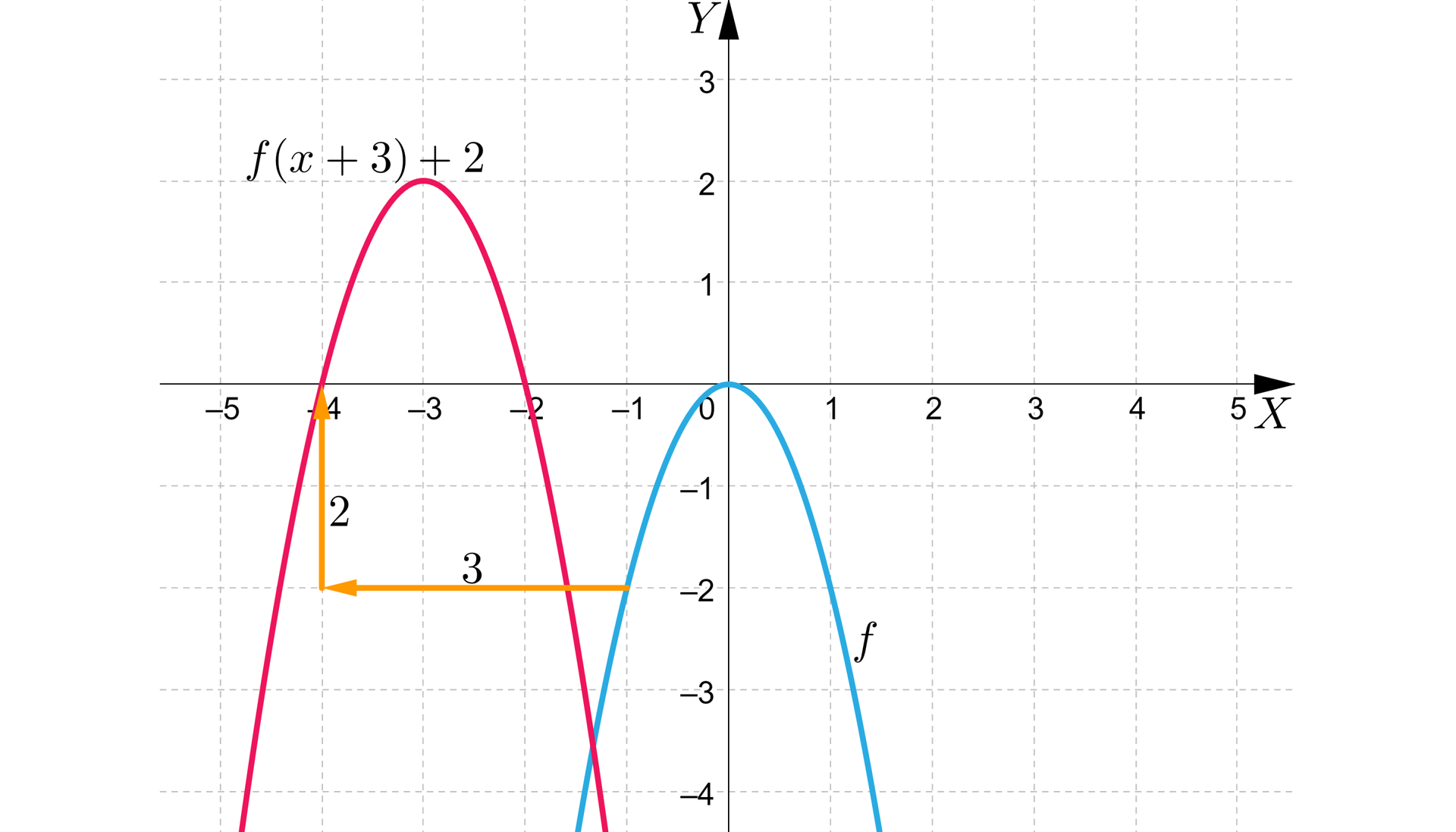
Zauważmy, że przy przesunięciu wykresu funkcji $f$ o $3$ jednostki w lewo wzdłuż osi $X$ i $2$ jednostkę w górę wzdłuż osi $Y$ otrzymujemy wykres funkcji $g$ o następujących własnościach:

zbiór wartości funkcji: $(- \infty, 2⟩$ ,
współrzędne wierzchołka paraboli, będącej wykresem funkcji $g$ : $(- 3, 2)$ ,
równanie osi symetrii paraboli, będącej wykresem funkcji $x = - 3$ ,
funkcja $g$ jest rosnąca w przedziale $(- \infty, - 3⟩$ ,
funkcja $g$ jest malejąca w przedziale $⟨- 3, \infty)$ ,
wartość największa funkcji $g$ wynosi $2$ dla $x = - 3$ .

Jeżeli przesuwamy parabolę, będącą wykresem funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej $f$ określonej wzorem $f (x) = a x^{2}$ , gdzie $a < 0$ , wzdłuż osi $X$ o $p$ jednostek w prawo lub o $p$ jednostek w lewo oraz wzdłuż osi $Y$ o $q$ jednostek w górę lub o $q$ jednostek w dół, to otrzymujemy parabolę, będącą wykresem funkcji $g$ o następujących własnościach:

zbiór wartości funkcji: $(- \infty, q⟩$
współrzędne wierzchołka paraboli, będącej wykresem funkcji $g$ : $(p, q)$ ,
równanie osi symetrii paraboli, będącej wykresem funkcji $g$ : $x = p$ ,
funkcja $g$ jest rosnąca w przedziale $(- \infty, p⟩$ ,
funkcja $g$ jest malejąca w przedziale $⟨p, \infty)$ ,
wartość największa funkcji $g$ wynosi $q$ dla $x = p$ .

Wnioski:

jeżeli parabolę, będącą wykresem funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej $f$ określonej wzorem $f (x) = a x^{2}$ , gdzie $a \in ℝ$ oraz $a \neq 0$ , przesuniemy o $p$ jednostek w prawo lub w lewo wzdłuż osi $X$ oraz o $q$ jednostek w górę lub w dół wzdłuż osi $Y$ , to otrzymamy parabolę, będącą wykresem funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej $g$ określonej wzorem $g (x) = a {(x - p)}^{2} + q$ ,
parabolę, będącą wykresem funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej $g$ określonej wzorem $g (x) = a {(x - p)}^{2} + q$ otrzymujemy w wyniku przesunięcia paraboli, będącej wykresem funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej $f$ określonej wzorem $f (x) = a x^{2}$ , gdzie $a \in ℝ$ oraz $a \neq 0$ o wektor o współrzędnych $[p, q]$ .

Przykład 1

Parabolę, będącą wykresem funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej $f$ określonej wzorem $f (x) = - \sqrt{2} x^{2}$ przesunięto o $3$ jednostki w lewo wzdłuż osi $X$ oraz o $1$ jednostkę w górę wzdłuż osi $Y$ i otrzymano parabolę, będącą wykresem funkcji $g$ .

RP31UaRxPv5kY

Ilustracja przedstawia poziomą oś X od minus siedmiu do trzech oraz pionową oś Y od minus dwóch do dwóch. Na rysunku zaznaczono także wykres funkcji kwadratowej f będącą parabolą z wierzchołkiem w punkcie nawias zero średnik zero koniec nawiasu oraz z ramionami skierowanymi w dół. Na ilustracji zaznaczono także wykres funkcji kwadratowej g będącym wykresem funkcji f przesuniętej o wektor nawias kwadratowy minus trzy średnik jeden koniec nawiasu. Wykres funkcji g posiada wierzchołek w punkcie nawias minus trzy średnik jeden koniec nawiasu oraz posiada ramiona skierowane w dół.

Wyznaczymy:

a) oś symetrii paraboli, będącej wykresem funkcji $g$ ,

b) współrzędne wierzchołka paraboli, będącej wykresem funkcji $g$ ,

c) zbiór wartości funkcji $g$ .

Rozwiązanie:

a) osią symetrii paraboli, będącej wykresem funkcji $g$ jest prosta o równaniu $x = - 3$ ,

b) wierzchołek paraboli, będącej wykresem funkcji $g$ ma współrzędne $(- 3, 1)$ ,

c) zbiorem wartości funkcji $g$ jest przedział $(- \infty, 1⟩$ .

Przykład 2

Parabolę, będącą wykresem funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej $g$ określonej wzorem $g (x) = - 3 x^{2}$ przesunięto wzdłuż osi $X$ i $Y$ i otrzymano parabolę, będącą wykresem funkcji $f$ .

RGTCWQBTk3lIV

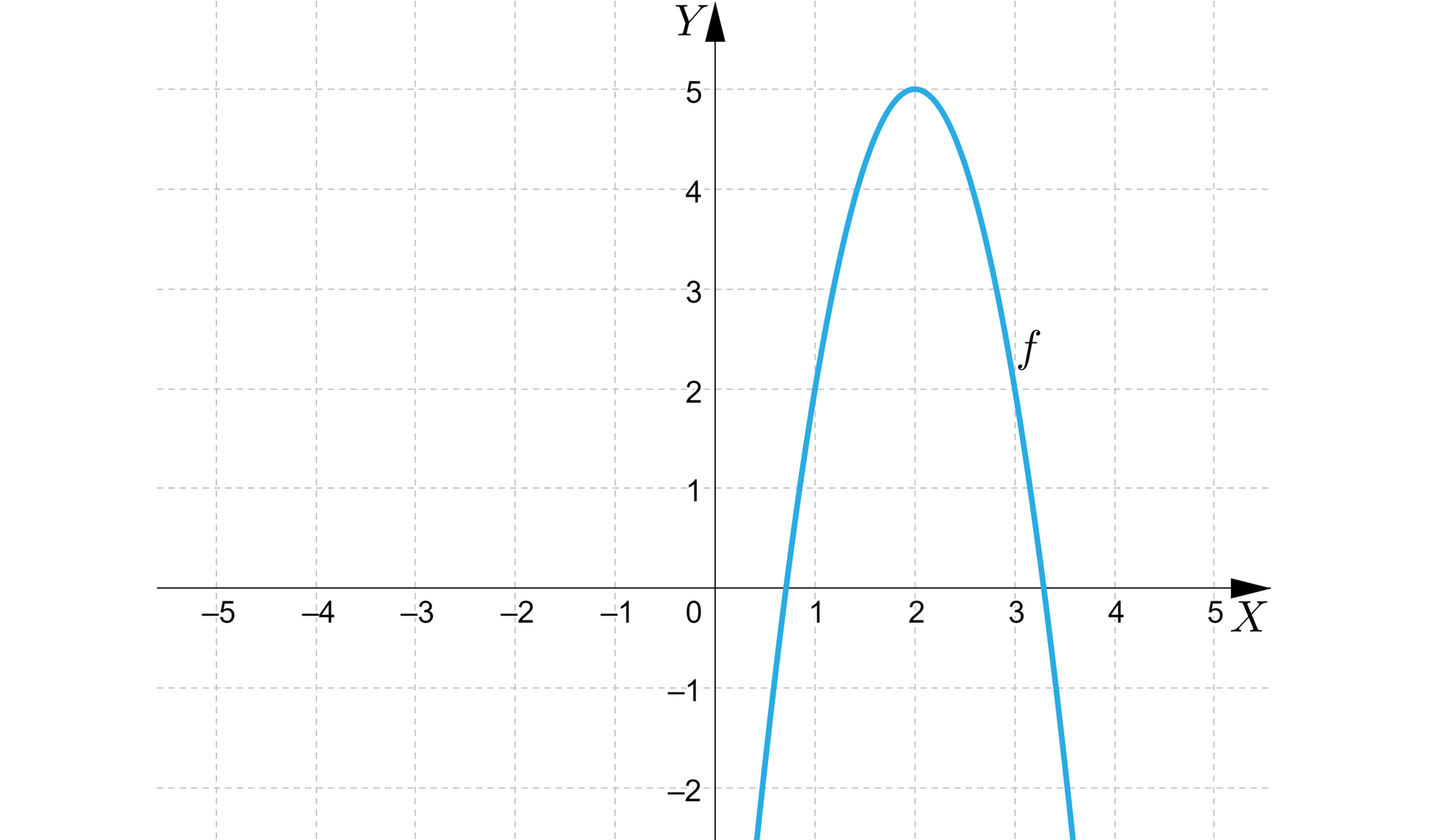
Ilustracja przedstawia poziomą oś X od minus pięciu do pięciu oraz pionową oś Y od minus dwóch do pięciu. Na rysunku zaznaczono także wykres funkcji kwadratowej f będącej parabolą o wierzchołku w punkcie nawias dwa średnik pięć koniec nawiasu oraz z ramionami skierowanymi w dół. Wykres funkcji posiada dwa miejsca zerowe i przechodzi przez punkty nawias jeden średnik dwa koniec nawiasu oraz nawias trzy średnik dwa koniec nawiasu.

Wyznaczymy:

a) współrzędne wektora przesunięcia wykresu funkcji $g$ ,

b) zbiór wartości funkcji $f$ .

Rozwiązanie:

Z wykresu odczytujemy, że wierzchołek paraboli, będącej wykresem funkcji $f$ ma współrzędne $(2, 5)$ , zatem:

a) współrzędne wektora przesunięcia wykresu funkcji $g$ , to $[2, 5]$ ,

b) zbiorem wartości funkcji $f$ jest przedział $(- \infty, 5⟩$ .

Przykład 3

Parabolę, będącą wykresem funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej $f$ określonej wzorem $f (x) = a x^{2}$ , dla $a > 0$ , przesunięto o $3$ jednostki w prawo wzdłuż osi $X$ i $2$ jednostki w górę wzdłuż osi $Y$ , a następnie o $4$ jednostki w lewo wzdłuż osi $X$ i $1$ jednostkę w dół wzdłuż osi $Y$ i otrzymano parabolę, będącą wykresem funkcji $g$ .

Wyznaczymy:

a) współrzędne wierzchołka paraboli, która jest wykresem funkcji $g$ ,

b) przedziały monotoniczności funkcji $g$ .

Rozwiązanie:

Zauważmy, że wykonanie omawianych przekształceńprzekształcenie wykresu funkcji $f (x - p) + q$ przekształceń wykresu funkcji $f$ sprowadza się do przesunięcia tego wykresu o $1$ jednostkę w lewo wzdłuż osi $X$ oraz o $1$ jednostkę w górę wzdłuż osi $Y$ .

Zatem:

a) wierzchołek paraboli, będącej wykresem funkcji $g$ ma współrzędne $(- 1, 1)$ ,

b) funkcja $g$ jest:

malejąca w przedziale $(- \infty, - 1⟩$ ,
rosnąca w przedziale $⟨- 1, \infty)$ .

Przykład 4

Dana jest funkcja kwadratowafunkcja kwadratowafunkcja kwadratowa $f$ określona wzorem $f (x) = - x^{2}$ . Parabolę, będącą wykresem tej funkcji przesunięto o $2$ jednostki w lewo wzdłuż osi $X$ oraz o $3$ jednostki w dół wzdłuż osi $Y$ i otrzymano wykres funkcji $g$ . Określimy liczbę rozwiązań równania $g (x) = m$ , dla $m \in ℝ$ .

RoY0iNgA6WjNB

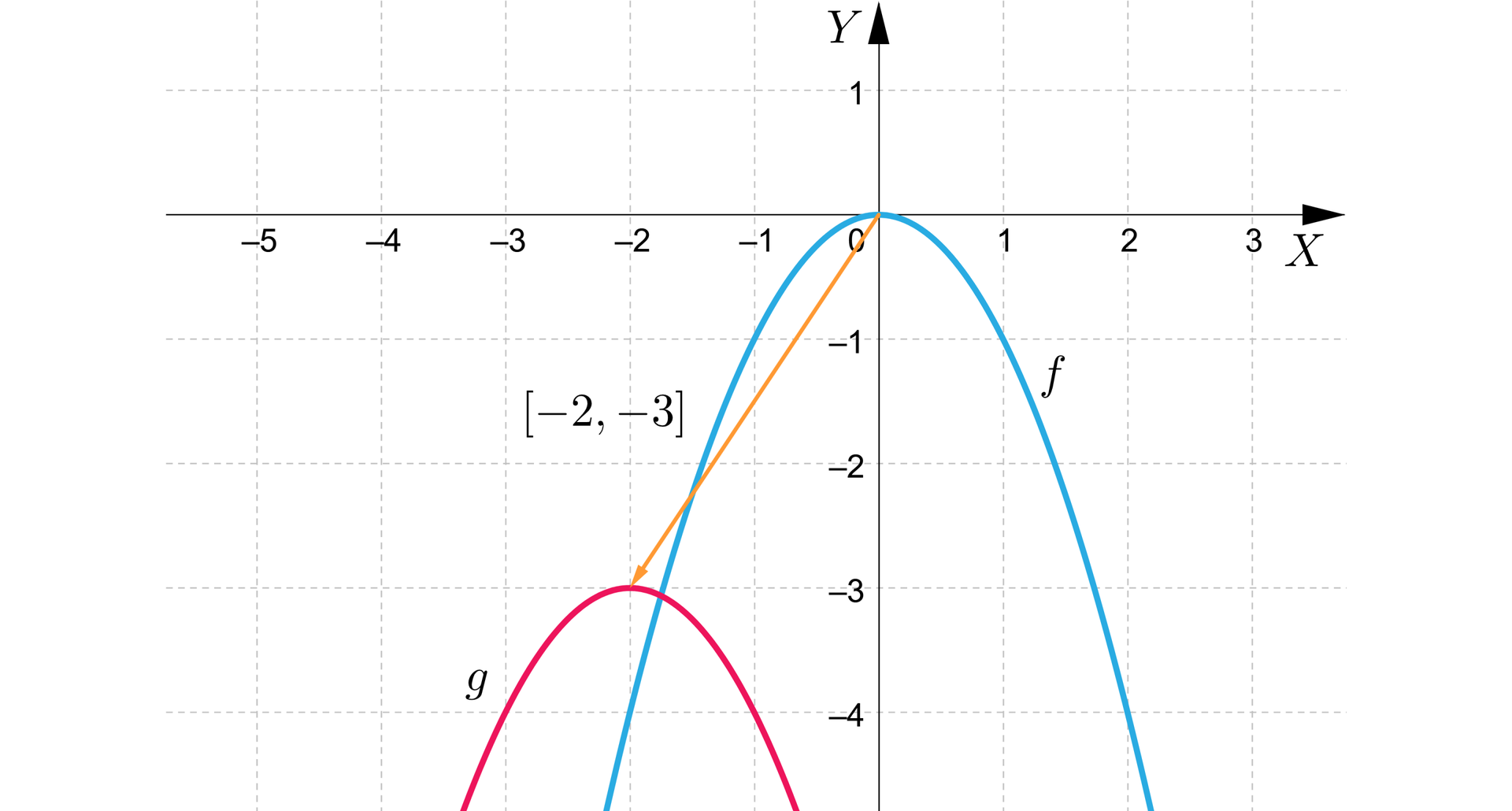
Ilustracja przedstawia poziomą oś X od minus pięciu do trzech oraz pionową oś Y od minus czterech do dwóch. Na rysunku zaznaczono także wykres funkcji kwadratowej f będącą parabolą z wierzchołkiem w punkcie nawias zero średnik zero koniec nawiasu oraz z ramionami skierowanymi w dół. Wykres przechodzi przez punkty nawias minus jeden średnik minus jeden koniec nawiasu oraz nawias jeden średnik minus jeden koniec nawiasu. Na ilustracji zaznaczono także wykres funkcji kwadratowej g będącym wykresem funkcji f przesuniętej o wektor nawias kwadratowy minus dwa średnik minus trzy koniec nawiasu. Wykres funkcji g posiada wierzchołek w punkcie nawias minus dwa średnik minus trzy koniec nawiasu oraz posiada ramiona skierowane w dół.

Rozwiązanie:

Zauważmy, że ramiona paraboli, która jest wykresem funkcji $g$ są skierowane do dołu. Wierzchołkiem paraboli, będącej wykresem funkcji $g$ jest punkt o współrzędnych $(- 2, - 3)$ .

Zatem równanie $g (x) = m$ , dla $m \in ℝ$ :

ma dwa rozwiązania, gdy $m \in (- \infty, - 3)$ ,
jedno rozwiązanie, gdy $m = - 3$ ,
nie ma rozwiązania, gdy $m \in (- 3, \infty)$ .

Przykład 5

Wyznaczymy, o jaki wektor należy przesunąć parabolę, będącą wykresem funkcji $f$ określonej wzorem $f (x) = x^{2}$ , aby otrzymać parabolę, będącą wykresem funkcji $g$ , do której należą punkty o współrzędnych $(- 1, - 3)$ oraz $(1, 5)$ .

Rozwiązanie:

Załóżmy, że wektor przesunięcia wykresu funkcji $f$ ma współrzędne $[p, q]$ .

Wobec tego funkcja $g$ jest określona wzorem $g (x) = {(x - p)}^{2} + q$ .

Ponieważ do paraboli, będącej wykresem funkcji $g$ należą punkty o współrzędnych $(- 1, - 3)$ oraz $(1, 5)$ , to do wyznaczenia wartości $p$ i $q$ rozwiązujemy układ równań:

$\{\begin{cases} - 3 = {(- 1 - p)}^{2} + q \\ 5 = {(1 - p)}^{2} + q \end{cases}$

Układ równań przekształcamy do postaci:

$\{\begin{cases} - q = {(- 1 - p)}^{2} + 3 \\ - q = {(1 - p)}^{2} - 5 \end{cases}$

Zatem:

${(- 1 - p)}^{2} + 3 = {(1 - p)}^{2} - 5$

$1 + 2 p + p^{2} + 3 = 1 - 2 p + p^{2} - 5$

$2 p + 3 = - 2 p - 5$

$4 p = - 8$

Wobec tego $p = - 2$ .

Obliczamy wartość $q$ :

$- q = {(- 1 - (- 2))}^{2} + 3 = 4$

$q = - 4$

Zatem wykres funkcji $f$ należy przesunąć o wektor $[- 2, - 4]$ .

Przykład 6

Wykres funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej $g$ otrzymujemy przez przesunięcie wykresu funkcji kwadratowej $f$ określonej wzorem $f (x) = 2 x^{2} - 4 x + 6$ o wektor o współrzędnych $[3, - 2]$ . Wyznaczymy najmniejszą wartość funkcji $g$ .

Rozwiązanie:

Zapiszmy wzór funkcji $f$ w postaci kanonicznej:

$f (x) = 2 x^{2} - 4 x + 6 = 2 \cdot (x^{2} - 2 x + 1) + 4 = 2 \cdot {(x - 1)}^{2} + 4$

Jeżeli wykres funkcji $f$ przesuniemy o wektor o współrzędnych $[3, - 2]$ , to otrzymujemy wykres funkcji $g$ określonej wzorem:

$g (x) = 2 \cdot {(x - 1 - 3)}^{2} + 4 - 2 = 2 \cdot {(x - 4)}^{2} + 2$

Wykres funkcji $g$ jest parabola, której wierzchołkiem jest punkt o współrzędnych $(4, 2)$ .

Ramiona paraboli, będącej wykresem funkcji $g$ są skierowane do góry.

Wobec tego funkcja $g$ osiąga wartość najmniejszą równą $2$ dla argumentu $4$ .

Słownik

funkcja kwadratowa

funkcja określona na zbiorze $ℝ$ wzorem $f (x) = a x^{2} + b x + c$ , gdzie $a$ , $b$ , $c \in ℝ$ oraz $a \neq 0$

przekształcenie wykresu funkcji

f (x - p) + q

przekształcenie wykresu funkcji

f (x - p) + q

przesunięcie wykresu funkcji $f$ wzdłuż osi $X$ o $p$ jednostek w prawo ( $p > 0$ ) lub o $p$ jednostek w lewo ( $p < 0$ ) oraz wzdłuż osi $Y$ o $q$ jednostek w górę, gdy $q > 0$ lub o $q$ jednostek w dół, gdy $q < 0$

Wprowadzenie

Symulacja interaktywna

Słownik