Przeczytaj
Zaczniemy od przypomnienia określenia dziedziny funkcji.
Dziedziną funkcji liczbowejfunkcji liczbowej nazywamy zbiór argumentów, dla których funkcja jest określona.
Czy dziedziną funkcji zawsze muszą być liczby rzeczywiste? Oczywiście, że nie. Pokażemy kilka przykładów funkcji, których dziedziną nie są liczby rzeczywiste. Funkcje te opisane będą za pomocą tabelki lub grafu.
Na lekcjach chemii posługujemy się tabelką, która zawiera liczby atomowe pierwiastków. Liczba atomowa jest to liczba określająca, ile protonów znajduje się w jądrze danego atomu. Jest ona równa liczbie elektronów niezjonizowanego atomu.
Poniżej przedstawiona jest tabelka częściowa zawierająca liczby atomowe kilku pierwiastków.
Wskażemy dziedzinę tej funkcji, która symbolom pierwiastków przyporządkowuje liczby atomowe tych pierwiastków.
Symbol chemiczny | H | He | Li | Be | B | C | N | O | F | Ne | Na | Mg |
Nazwa | wodór | hel | lit | beryl | bor | węgiel | azot | tlen | fluor | neon | sód | magnez |
Liczba atomowa |
Rozwiązanie:
Dziedziną funkcji jest zbiór pierwiastków chemicznych.
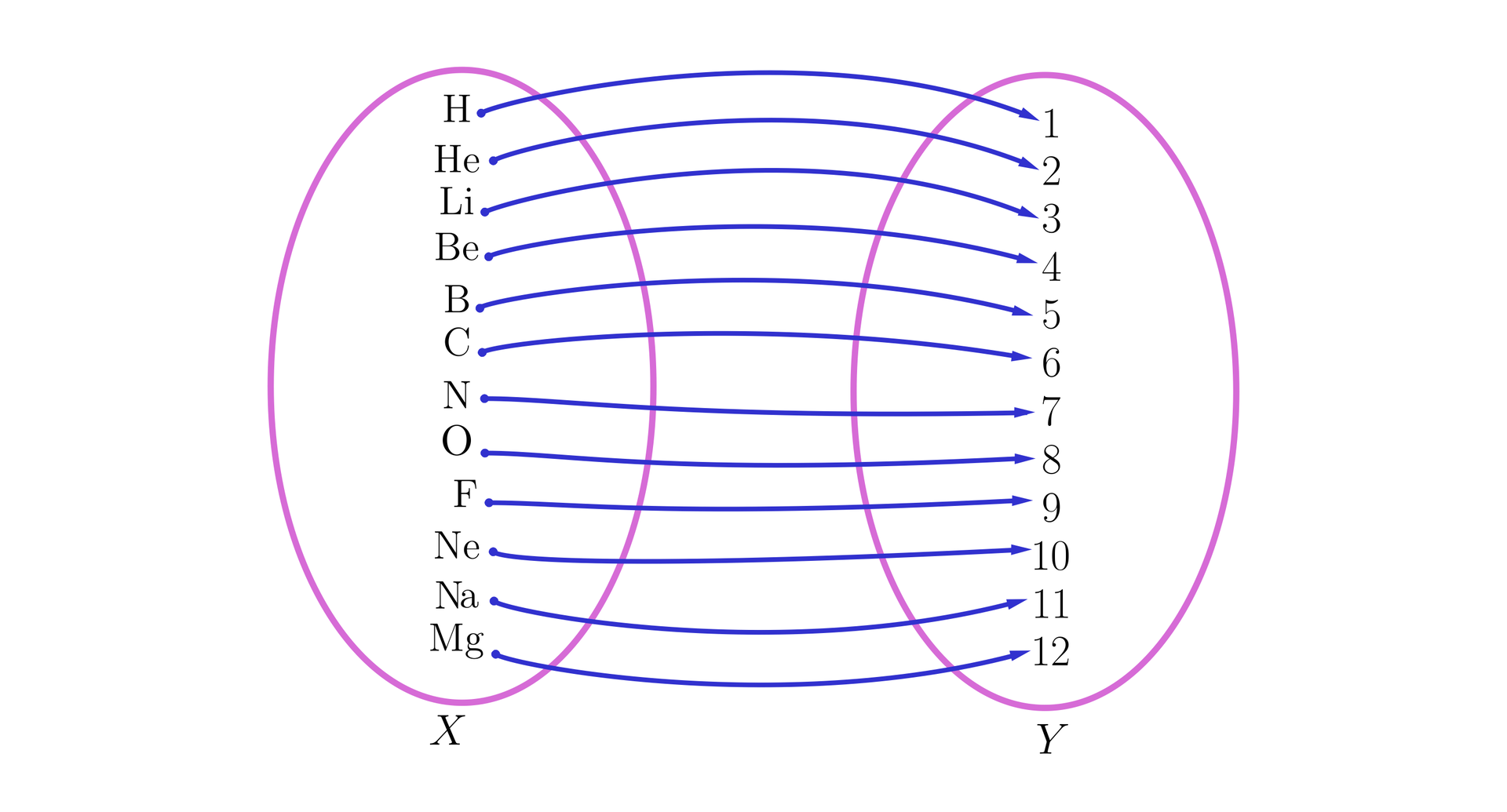
Możemy przedstawić tę funkcję w postaci grafu. Elementy dziedziny funkcji umieścimy w lewej części grafu.
Karolina jest uczennicą klasy pierwszej szkoły ponadpodstawowej. Wśród swoich koleżanek i kolegów przeprowadziła ankietę na temat ich zainteresowań pozaszkolnych. Wyniki ankiety przedstawiła w postaci grafu. Każdy uczestnik ankiety mógł wskazać tylko jeden interesujący go temat. Przeanalizujemy wyniki tego badania, sprawdzimy, czy jest to funkcja i wskażemy jej dziedzinę.
Rozwiązanie:

Powyższy graf przedstawia funkcję. Każdemu elementowi ze zbioru przyporządkowany jest dokładnie jeden element ze zbioru . Dziedziną tej funkcji jest zbiór uczniów:
Ania, Zosia, Kasia, Zuzia, Dominik, Daniel, Michał, Kuba, Antek, Tymon, Damian, Kinga, Klara, Paulina
Przedstawmy wyniki ankiety w postaci tabelki. Dziedzinę zapiszemy w lewej kolumnie.
Dziedzina | Wartości funkcji |
|---|---|
Ania | taniec |
Zosia | nauka języków obcych |
Kasia | śpiew |
Zuzia | sport |
Dominik | śpiew |
Daniel | sport |
Michał | balet |
Kuba | gra na instrumencie muzycznym |
Antek | sport |
Tymon | balet |
Damian | gra na instrumencie muzycznym |
Kinga | czytanie książek |
Klara | gra na instrumencie muzycznym |
Paulina | balet |
Funkcja przedstawiona jest za pomocą opisu słownego.
Funkcja każdej dwucyfrowej liczbie naturalnej należącej do przedziału przyporządkowuje sumę jej cyfr. Wykonajmy tabelkę oraz graf tej funkcji i wskażmy jej dziedzinę.
Rozwiązanie:
Tabelka funkcji .
Dziedziną funkcji są liczby zapisane w pierwszym wierszu tabelki.
Przedstawmy graf funkcji . Dziedzina funkcji umieszczona jest w lewej części grafu.

Przykłady pokazały, w jaki sposób określamy dziedzinę funkcji opisanej za pomocą tabelki lub grafu.
Jeżeli funkcja opisana jest za pomocą tabelki poziomej, to będziemy przyjmować, że do dziedziny funkcji należą elementy zapisane w pierwszym wierszu.
Jeżeli funkcja jest opisana za pomocą tabelki pionowej, to będziemy przyjmować, że do dziedziny funkcji należą elementy zapisane lewej kolumnie.
Jeżeli funkcja jest opisana za pomocą grafu, to będziemy przyjmować, że do dziedziny funkcji należą elementy zapisane w lewej części grafu.
Słownik
funkcja, której dziedzina i zbiór wartości to zbiory liczbowe