Rachunki pamięciowe na dużych liczbach

W naszym otoczeniu często spotykamy duże liczby. Ceny niektórych produktów zapisane są za pomocą liczb wielocyfrowych – rower kosztuje ponad $400 zł$ , a komputer około $4000 zł$ . Podróżując, pokonujemy duże odległości. Z Warszawy do Paryża jest $1400 km$ , a do Nowego Jorku $6900 km$ . Dzięki umiejętności liczenia na dużych liczbach wiemy, że komputer jest droższy od roweru $10$ razy, a Paryż jest o $5500 km$ bliżej Warszawy niż Nowy Jork.

Do rachunków na takich liczbach nie zawsze potrzebujemy kalkulatora, niektóre można wykonać w pamięci. Jeśli umiemy dodawać, odejmować, mnożyć i dzielić pamięciowo małe liczby, to powinniśmy poradzić sobie także z działaniami na niektórych większych liczbach.

Przykład 1

Rn1hfp0VtLE9H1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przykład 2

Jeśli wiemy, że $2 + 7 = 9$ , to dodawanie liczb $20$ i $70$ sprowadza się do dodania $2$ i $7$ oraz dopisania do wyniku, czyli $9$ , zera.

RIVyGXKdjzucz1

"Przykłady: 2 +7 =9 — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Analogicznie dodajemy $200$ i $700$ . Znów dodajemy $2$ i $7$ i dopisujemy do wyniku, czyli $9$ , dwa zera. Dodając $2 000$ i $7 000$ postępujemy tak samo. Dodajemy $2$ i $7$ , a do wyniku dopisujemy trzy zera.
Większe liczby dodajemy podobnie.

R5fioZ5UmtGP41

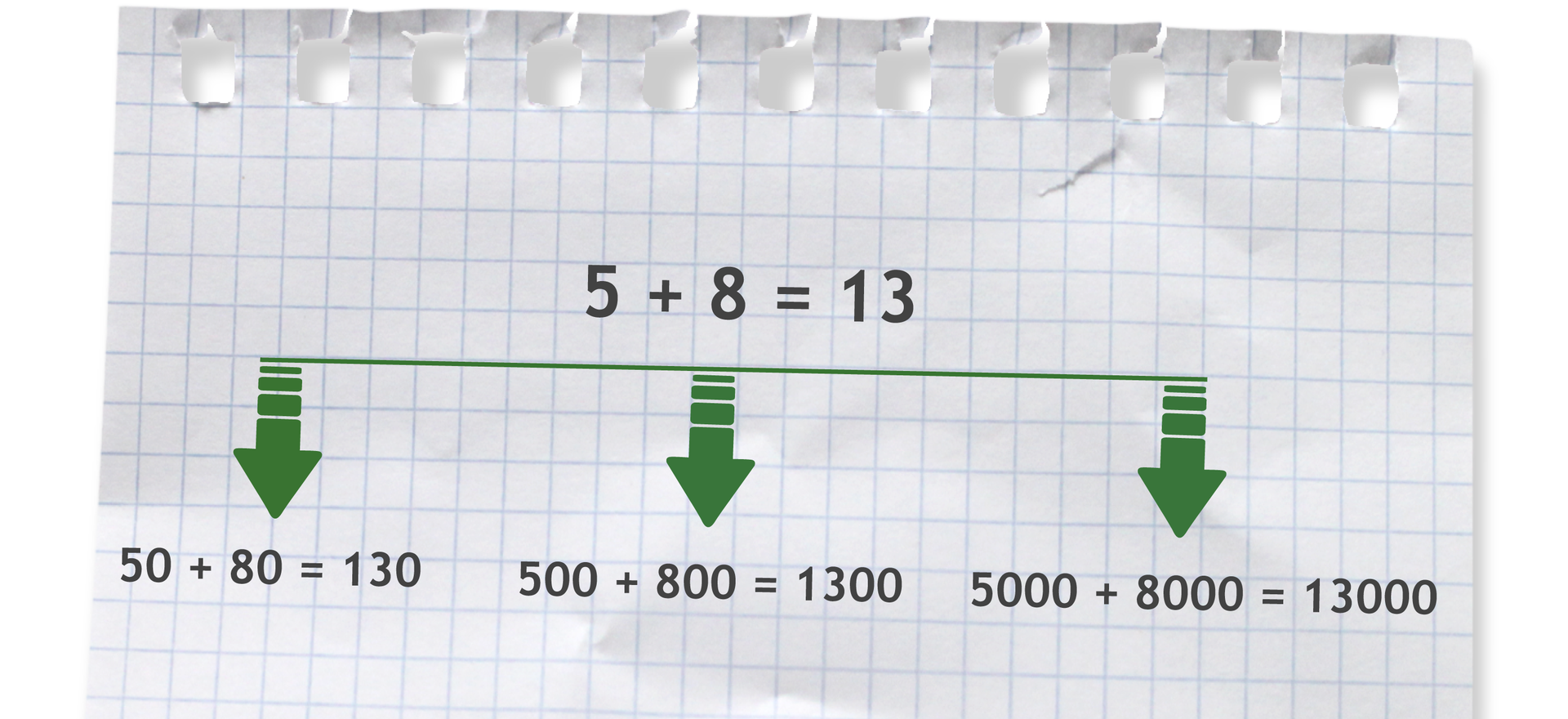
"Przykłady: 5 +8 =13 — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przykład 3

Podobnie jak w poprzednim przykładzie dodajemy większe liczby.

RiAVy4iqNmhkw1

"Przykłady: 35 +7 =42 — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przykład 4

RafZQIwGB6Kw91

Przykład 5

RU1z5kElmwgoV1

"Przykłady: 38 -12 =26 — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

classicmobile

Ćwiczenie 1

R1JgcRN3AXehc1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

static

Ćwiczenie 1

Uzupełnij zapisy sum.

RtDfSkK8lO4A81

Grafika statyczna — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

$88$
$000$
$84$
$81$
$00$
$109$
$00$
$000$
$16$
$459$

classicmobile

Ćwiczenie 2

RftHsiPbbuaof1

Uzupełnij.

a) $8 900 - 5 400 =$ ............ $00$
b) $76 000 - 15 000 =$ ............ $000$
c) $6 700 - 2 500 = 42$ ............
d) $4 200 000 - 4 100 000 =$ ............ $00 000$
e) $8 200 - 8 000 = 2$ ............
f) $36 000 - 27 000 = 9$ ............
g) $9 700 - 4 000 = 57$ ............
h) $830 000 - 8 000 =$ ............ $000$
i) $1 100 - 20 = 108$ ............
j) $22 200 - 500 = 217$ ............

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

static

Ćwiczenie 2

Uzupełnij zapisy różnic.

R1BFJ3UBQ91cO1

$35$
$61$
$00$
$1$
$00$
$000$
$00$
$822$
$0$
$00$

Ćwiczenie 3

RNZXgyxiMwZI81

Niektóre z podanych liczb są wynikami poniższych działań. Odpowiednio przeciągnij i upuść.

$53 000$ , $92 000$ , $62 000$ , $247 000$ , $30 000$ , $5 900$ , $10 000$ , $1 000$ , $5 300$ , $400 000$ , $2 100$ , $119 200$ , $11 600$ , $6 200$ , $40 000$ , $116 000$

$300 + 1 800 =$ ..................
$6 700 - 500 =$ ..................
$2 000 + 2 400 + 1 500 =$ ..................
$100 000 - 35 000 - 12 000 =$ ..................
$18 000 - 6 400 =$ ..................
$230 000 + 17 000 =$ ..................
$24 000 + 8 000 - 2 000 =$ ..................
$7 500 + 2 500 =$ ..................

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ciekawostka

Wiadomo, że

12 + 21 = 33 = 3 ∙ 11

123 + 321 = 444 = 4 ∙ 111

234 + 432 = 666 = 6 ∙ 111

123456 + 654321 = 777777 = 7 ∙ 111111

Zastanów się, jakich liczb dotyczy ta zależność. Czy wszystkich? A może składniki sum coś łączy? Podaj kilka kolejnych przykładów.

Jeśli potrafimy mnożyć w pamięci liczby w zakresie $100$ , to poradzimy sobie również z mnożeniem niektórych dużych liczb.
Najłatwiej mnożyć liczby przez $10, 100, 1000, 10 000$ itd.

Ćwiczenie 4

Wykonaj wskazane w tabeli mnożenia, używając kalkulatora i wpisz wyniki do tabeli.

Tabela. Dane
$•$	$3$	$7$	$13$	$45$	$72$	$105$	$238$
$10$
$100$
$1000$

Tabela. Dane
$•$	$3$	$7$	$13$	$45$	$72$	$105$	$238$
$10$	$30$	$70$	$130$	$450$	$720$	$1050$	$2380$
$100$	$300$	$700$	$1300$	$4500$	$7200$	$10500$	$23800$
$1000$	$3000$	$7000$	$13000$	$45000$	$72000$	$105000$	$238000$

Zapamiętaj!

Aby pomnożyć liczbę przez $10$ , wystarczy do tej liczby dopisać na jej końcu jedno zero.
Aby pomnożyć liczbę przez $100$ , wystarczy do tej liczby dopisać na jej końcu dwa zera.
Aby pomnożyć liczbę przez $1000$ , wystarczy do tej liczby dopisać na jej końcu trzy zera.
Aby pomnożyć liczbę przez $10000$ , wystarczy do tej liczby dopisać na jej końcu cztery zera.

Przykład 6

Jak pomnożyć daną liczbę przez $20, 30, 40, 50$ , … lub przez $200, 300, 400, 500$ , … ? Czy jest to równie proste?

Rg1aUE8vTPX7H1

Przykład 7

R16Ylj3NmDHgS1

Ważne!

Jeśli mnożymy liczby, które są zakończone zerami, to

mnożymy liczby, które zostaną po odrzuceniu zer,
do otrzymanego wyniku dopisujemy tyle zer, ile łącznie odrzuciliśmy.

classicmobile

Ćwiczenie 5

R129NOqrqp4vO1

Przeciągnij i upuść.

300, , 9 000, 0 000, 000, 35, 350, 16 000 000, 80, 800, 1 600 000, 3 000, 900

a) $30 \cdot 600 = 18$ ....................
b) $500 \cdot 700 =$ .................... $0 000$
c) $200 \cdot 8 000 = ....................
d)$ $400 \cdot$ .................... $= 360 000$
e) .................... $\cdot 2 000 = 160 000$
f) $70 \cdot$ .................... $= 21 000$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

static

Ćwiczenie 5

Uzupełnij zapisy iloczynów.

RcZSraYOBq9o41

$000$
$35$
$1 600 000$
$900$
$80$
$300$

Przykład 8

Dzielenie i mnożenie są działaniami wzajemnie odwrotnymi, stąd

$13 \cdot 10 = 130$ , zatem $130 : 10 = 13$
$50 \cdot 10 = 500$ , zatem $500 : 10 = 50$
$2700 \cdot 10 = 27 000$ , zatem $2 7000 : 10 = 2700$
$4000 \cdot 10 = 40 000$ , zatem $40 000 : 10 = 4000$

Porównaj zapis dzielnej i ilorazu. Czym różnią się zapisy tych liczb?

Ważne!

Jeżeli dzielimy przez $10$ liczbę zakończoną zerem (lub zerami), to jako wynik zapisujemy dzielną bez jednego zera na końcu.

Przykład 9

Dzielenie przez $100$ możemy zastąpić dwukrotnym dzieleniem przez $10$ .

$4500 : 100 = (4500 : 10) : 10 = 450 : 10 = 45$ , czyli $4500 : 100 = 45$
$6000 : 100 = (6000 : 10) : 10 = 600 : 10 = 60$ , czyli $6000 : 100 = 60$
$970 000 : 100 = (970 000 : 10) : 10 = 970000 : 10 = 9700$ , czyli $970 000 : 100 = 9700$

Porównaj zapis dzielnej i ilorazu. Czym teraz różnią się zapisy tych liczb?

Ważne!

Jeżeli dzielimy przez $100$ liczbę zakończoną zerami, to jako wynik zapisujemy dzielną z opuszczonymi na końcu dwoma zerami.
Podobnie zapisujemy wynik dzielenia przez $1000, 10000, 100000$ …. Wynikiem jest odpowiednio dzielna bez trzech, czterech, pięciu, … zer na końcu.

Przykład 10

RmTKuRDH8DkQk1

Przykład 11

Przyjrzyj się poniższym przykładom, w których pokazano, jak można ułatwić dzieleniem, gdy w dzielnej i dzielniku jest inna liczba zer.

$2400 : 8 = 300$
$1800 : 20 = 180 : 2 = 90$
$5 600 000 : 28 000 = 5600 : 28 = 200$

classicmobile

Ćwiczenie 6

Rhq3Dh8xOBNfK1

Uzupełnij.

a) $270 : 10 =$ ............
b) $1 450 : 10 =$ ............
c) $2 400 : 100 =$ ............
d) $7 600 : 10 =$ ............
e) ............ $: 1 000 = 23$
f) $4 600 : =$ ............ $= 46$
g) $590 000 =$ ............ $= 590$
h) ............ $: 10 = 3200$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

static

Ćwiczenie 6

Uzupełnij zapisy ilorazów.

RZqsuURMZtrTj1

$27$
$145$
$24$
$760$
$23000$
$100$
$1000$
$32000$

classicmobile

Ćwiczenie 7

ReDpEjczkaLFJ1

Uzupełnij.

a) 2800 : 400 = ............
b) 480 : 60 = ............
c) 2600 : 200 = ............
d) 81000 : 9000 = ............
e) 3000 : 500 = ............
f) ............ : 300 = 5
g) ............ : 70 = 60
h) 35000 : ............ = 50

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

static

Ćwiczenie 8

RxKZiv46H53Sk1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

classicmobile

Ćwiczenie 9

R1Pjn7NUdCjmu1

Nie wykonując obliczeń, uzupełnij znakiem: >, < lub =.

a) 1100 + 2600 ............ 990 + 2600
b) 90000 + 20000 ............ 1000000
c) 8400 – 2500 ............ 8400 – 2400
d) 10000 – 1 ............ 999 + 999
e) 360 : 40 ............ 3600 : 400
f) 50∙600 ............ 3000

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

static

Ćwiczenie 9

Nie wykonując obliczeń, porównaj liczby. W prostokąt wstaw odpowiedni znak: $>, <$ lub $= .$

R1bz4GWhBHqWi1

classicmobile

Ćwiczenie 10

RpcWyb5pECQfm1

Pan Kowalski kilka razy w tygodniu wypłacał pieniądze z banku.

Uzupełnij.

W poniedziałek otrzymał 10 banknotów po 100 zł , czyli ............ zł.
We wtorek otrzymał 100 banknotów po 50 zł, czyli ............ zł.
W czwartek otrzymał 350 banknotów po 10 zł, czyli ............ zł.
W piątek otrzymał 30 banknotów po 200 zł, czyli ............ zł.
W sobotę pan Kowalski obliczył, że w ciągu tego tygodnia wypłacił razem ............ zł.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

static

Ćwiczenie 10

R17ILGNSBmjJ41

Pn: $1 000$
wt: $5 000$
czw : $3 500$
pt : $6 000$
tydzień : $15 500$

classicmobile

Ćwiczenie 11

R1NAUrgCqOXxU1

Pani Jola, mieszkanka Warszawy, postanowiła zwiedzić kilka innych stolic. Najpierw poleciała do Tokio, a stamtąd do Pekinu. Przed powrotem do Warszawy zwiedziła jeszcze Kair. W informacji turystycznej dowiedziała się, że z Warszawy do Tokio jest 8 600 km, z Tokio do Pekinu – 2 100 km, z Pekinu do Kairu – 7 500 km, a z Kairu do Warszawy – 2 600 km. Jaką łączną długość miała trasa, którą pokonała pani Jola podczas tej wycieczki?

............ km

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

static

Ćwiczenie 11

Pani Jola, mieszkanka Warszawy, postanowiła zwiedzić kilka innych stolic. Najpierw poleciała do Tokio, a stamtąd do Pekinu. Przed powrotem do Warszawy zwiedziła jeszcze Kair. W informacji turystycznej dowiedziała się, że z Warszawy do Tokio jest $8600 km$ , z Tokio do Pekinu – $2100 km$ , z Pekinu do Kairu – $7500 km$ , a z Kairu do Warszawy – $2600 km$ . Jaką łącznie odległość pokonała pani Jola podczas tej wycieczki?

$20 800 km$

Ciekawostka

Łatwo możemy pomnożyć w pamięci dwie liczby dwucyfrowe trochę mniejsze od $100$ , na przykład $96$ i $95$ .
Aby wykonać takie działanie, musimy najpierw znaleźć liczby, które są dopełnieniami czynników do $100$ , czyli w przypadku $96$ jest to $4$ (tyle brakuje do $100$ ), a w przypadku $95$ jest to $5$ (tyle brakuje do $100$ ).
Mamy następującą sytuację:

\overset{4}{\overset{⏞}{96}} ∙ \overset{5}{\overset{⏞}{95}} =

Zaczynamy zapisywać wynik tego mnożenia.

Odejmujemy od dowolnego czynnika liczbę, która jest dopełnieniem drugiego czynnika. Otrzymujemy liczbę $91 (96 - 5$ lub $95 - 4)$ , która jest początkiem wyniku mnożenia.
Następnie do tej liczby dopisujemy iloczyn liczb, które są dopełnieniami, czyli $20$ $(4 ∙ 5)$ . Gdy iloczyn dopełnień jest liczbą jednocyfrową , poprzedzamy go cyfrą $0$ .

\overset{4}{\overset{⏞}{96}} ∙ \overset{5}{\overset{⏞}{95}} = 9120

W ten sposób można wprawdzie mnożyć dowolne liczby dwucyfrowe, ale gdy są one znacznie mniejsze niż $100$ , to rachunki pamięciowe są uciążliwe.
Spróbuj pomnożyć w ten sposób inne liczby.

Zaokrąglanie liczb naturalnych

Zapisywanie liczb w systemie rzymskim