Współczynnik kierunkowy funkcji liniowej
Ten materiał jest dobrym wprowadzeniem do zadań o funkcji liniowej. Możesz je znaleźć w materiałach:
Zadania obliczeniowe oraz wyznaczanie wzoru funkcji na podstawie jej wykresuZadania obliczeniowe oraz wyznaczanie wzoru funkcji na podstawie jej wykresu,
Odczytywanie i obliczanie argumentów oraz wartości funkcjiOdczytywanie i obliczanie argumentów oraz wartości funkcji,
Zadania obliczeniowe dotyczące funkcji liniowej. Część IZadania obliczeniowe dotyczące funkcji liniowej. Część I.
Rozpatrzmy funkcję liniową określoną wzorem
Ponieważ oraz , zatem wykres funkcji przecina oś w punkcie i przechodzi przez punkt .

Pokażemy, że przy zwiększaniu argumentu o odpowiadająca mu wartość funkcji zwiększa się o .
Weźmy dowolną liczbę rzeczywistą . Wtedy
a także
Obliczamy różnicę tych dwóch wartości
Punkt jest dowolnym punktem należącym do wykresu funkcji . Aby znaleźć punkt , którego pierwsza współrzędna jest o większa od pierwszej współrzędnej punktu , przesuwamy się o jednostkę wzdłuż osi i o jednostki wzdłuż
osi .

Film dostępny pod adresem /preview/resource/RBTDXwPyCxSF9
Animacja pokazuje na wykresie funkcji f(x) = 2x -1, że zwiększając argument o 1 zwiększa się odpowiadająca mu wartość funkcji f o 2.
Rozpatrzmy funkcję liniową określoną wzorem
Ponieważ oraz , to wykres funkcji przecina oś w punkcie i przechodzi przez punkt .

Pokażemy, że przy zwiększaniu argumentu o odpowiadająca mu wartość funkcji zmniejsza się o .
Weźmy dowolną liczbę rzeczywistą . Wtedy
a także
Obliczamy różnicę tych dwóch wartości
Wobec tego, wybierając dowolny punkt na wykresie funkcji , znajdziemy na wykresie inny punkt, który powstaje z przesunięcia punktu o jednostkę wzdłuż osi i o jednostkę wzdłuż osi .

Film dostępny pod adresem /preview/resource/RYbicJSbrZDh5
Animacja pokazuje na wykresie funkcji f(x) = minus x +1, że zwiększając argument o 1 zmniejsza się odpowiadająca mu wartość funkcji f o 1.
Rozpatrzmy funkcję liniową określoną wzorem
Ponieważ oraz , to wykres funkcji przecina oś w punkcie i przechodzi przez punkt .

Pokażemy, że przy zwiększaniu argumentu o odpowiadająca mu wartość funkcji zmniejsza się o .
Weźmy dowolną liczbę rzeczywistą . Wtedy
a także
Obliczamy różnicę tych dwóch wartości
Wobec tego, wybierając dowolny punkt na wykresie funkcji , znajdziemy na wykresie inny punkt, który powstaje z przesunięcia punktu o jednostkę wzdłuż osi i o jednostki wzdłuż osi . Można też znaleźć kolejny punkt, który powstaje z przesunięcia punktu o jednostki wzdłuż osi i o jednostkę wzdłuż osi .

Film dostępny pod adresem /preview/resource/Rcbfu36wRtW4Y
Animacja pokazuje na wykresie funkcji f(x) = minus jedna druga x +2, że zwiększając argument o 1 zmniejsza się odpowiadająca mu wartość funkcji f o jedną drugą.
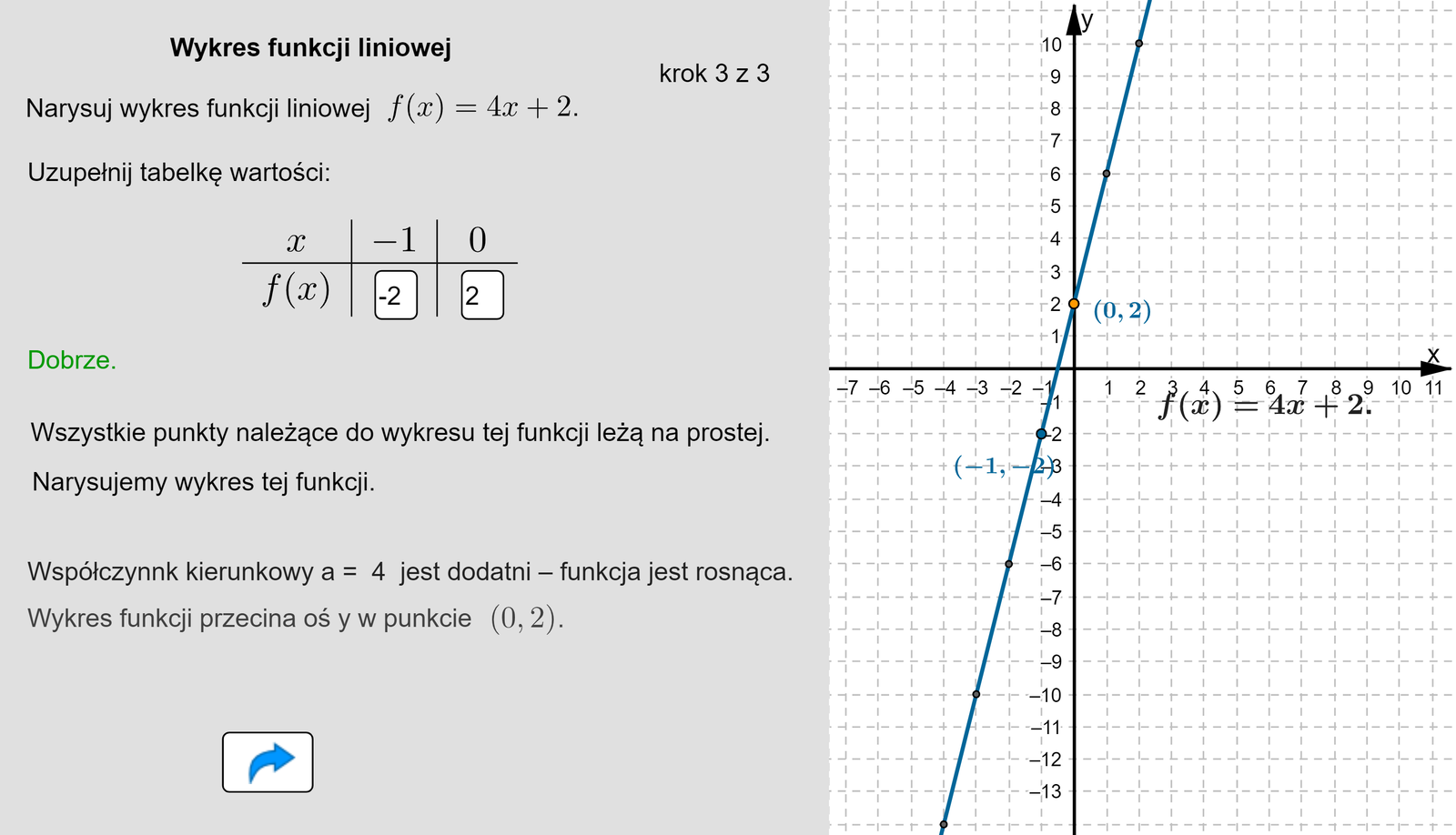
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PLN5fvTTh
Wybierzmy na wykresie funkcji liniowej różne punkty i , o współrzędnych i . Wtedy
,
.
Zauważmy, że , a także , więc , skąd . Zatem
Ponieważ punkty i są różne i leżą na wykresie funkcji, więc , stąd . Wobec tego
jest ilorazem różnicy dwóch wartości funkcji liniowej przez różnicę odpowiadających im argumentów.
Patrząc na dwa różne punkty i , leżące na wykresie funkcji
interpretujemy współczynnik kierunkowy jako iloraz wartości przesunięcia wzdłuż osi do odpowiadającej mu wartości przesunięcia wzdłuż osi .

Film dostępny pod adresem /preview/resource/Rj4zDTvVdkssC
Animacja pokazuje powyżej opisaną interpretację geometryczną współczynnika kierunkowego a funkcji liniowej f(x) = a razy x +b.
Na wykresie funkcji liniowej leżą punkty i . Ponieważ
więc współczynnik kierunkowy tej funkcji jest równy
Liczba oznacza również, że wzrostowi argumentu funkcji o jedną jednostkę odpowiada wzrost wartości o jednostki.
Na wykresie funkcji liniowej leżą punkty i . Ponieważ
,
zatem współczynnik kierunkowy tej funkcji jest równy
Liczba oznacza również, że wzrostowi argumentu funkcji o jedną jednostkę odpowiada zmniejszenie wartości funkcji o jednostki.
Na wykresie funkcji liniowej leżą punkty i . Ponieważ
to współczynnik kierunkowy tej funkcji jest równy
Wartość oznacza również, że wzrostowi argumentu funkcji o jedną jednostkę, odpowiada wzrost wartości o .
Wykonaj polecenia zawarte w poniższym aplecie.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PLN5fvTTh
Zapoznaj się z wiadomościami zawartymi poniżej.
Każda prosta ma wzór ogólny . Parametr w tym wzorze to jej współczynnik kierunkowy i odpowiada on za nachylenie prostej do osi . Współczynnik odpowiada za przesunięcie prostej wzdłuż osi . Wybierając różne parametry funkcji możemy wpływać na jej wygląd. Rozważmy dwa przykłady:
Dla parametrów i wzór prostej to . Jest to prosta, która przechodzi przez pierwszą, trzecią i czwartą ćwiartkę układu współrzędnych, przecina oś w punkcie , a oś w punkcie .
Dla parametrów i wzór prostej to . Jest to prosta, która przechodzi przez pierwszą, drugą i czwartą ćwiartkę układu współrzędnych, przecina oś w punkcie , a oś w punkcie .
Z poniższego wzoru możemy obliczyć współczynnik kierunkowy prostej, jeżeli znamy dwa punkty, przez jakie ona przechodzi.
Rozważmy prostą, która przechodzi przez punkty i . Zgodnie ze wzorem, jej współczynnik kierunkowy wynosi , co pokrywa się z danymi z drugiego przykładu.