Monotoniczność funkcji
Obserwuj, jak przy zmianie argumentów zmieniają się wartości funkcji, o której mówimy, że jest funkcją rosnącą.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DRBFgBGnP
Obserwuj, jak przy zmianie argumentów zmieniają się wartości funkcji, o której mówimy, że jest funkcją malejącą.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DRBFgBGnP
Obserwuj, jak przy zmianie argumentów zmieniają się wartości funkcji, o której mówimy, że jest funkcją nierosnącą.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DRBFgBGnP
Obserwuj, jak przy zmianie argumentów zmieniają się wartości funkcji, o której mówimy, że jest funkcją niemalejącą.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DRBFgBGnP
Każdą z czterech prezentowanych w powyższych przykładach funkcji nazywać będziemy funkcją monotoniczną.
Funkcja jest określona w przedziale .
Jeżeli dla dowolnych takich, że spełniony jest warunek:
to mówimy, że funkcja jest rosnąca w przedziale .
Funkcja jest określona w przedziale .
Jeżeli dla dowolnych takich, że spełniony jest warunek:
to mówimy, że funkcja jest malejąca w przedziale .
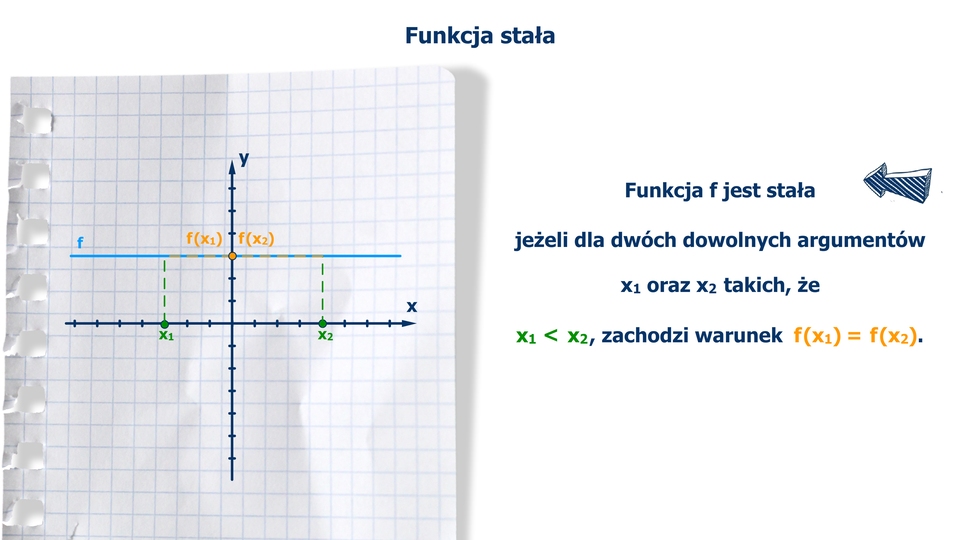
Jeżeli dla dowolnych takich, że spełniony jest warunek:
to funkcję nazywamy stałą w przedziale .
Jeżeli dla dowolnych takich, że spełniony jest warunek:
to mówimy, że funkcja jest niemalejąca w przedziale .
Jeżeli dla dowolnych takich, że spełniony jest warunek:
To mówimy, że funkcja jest nierosnąca w przedziale
Jeśli funkcja, której dziedzinę można podzielić na rozłączne przedziały tak, aby w każdym z nich funkcja ta była monotoniczna, to powiemy, że jest ona monotoniczna przedziałami.
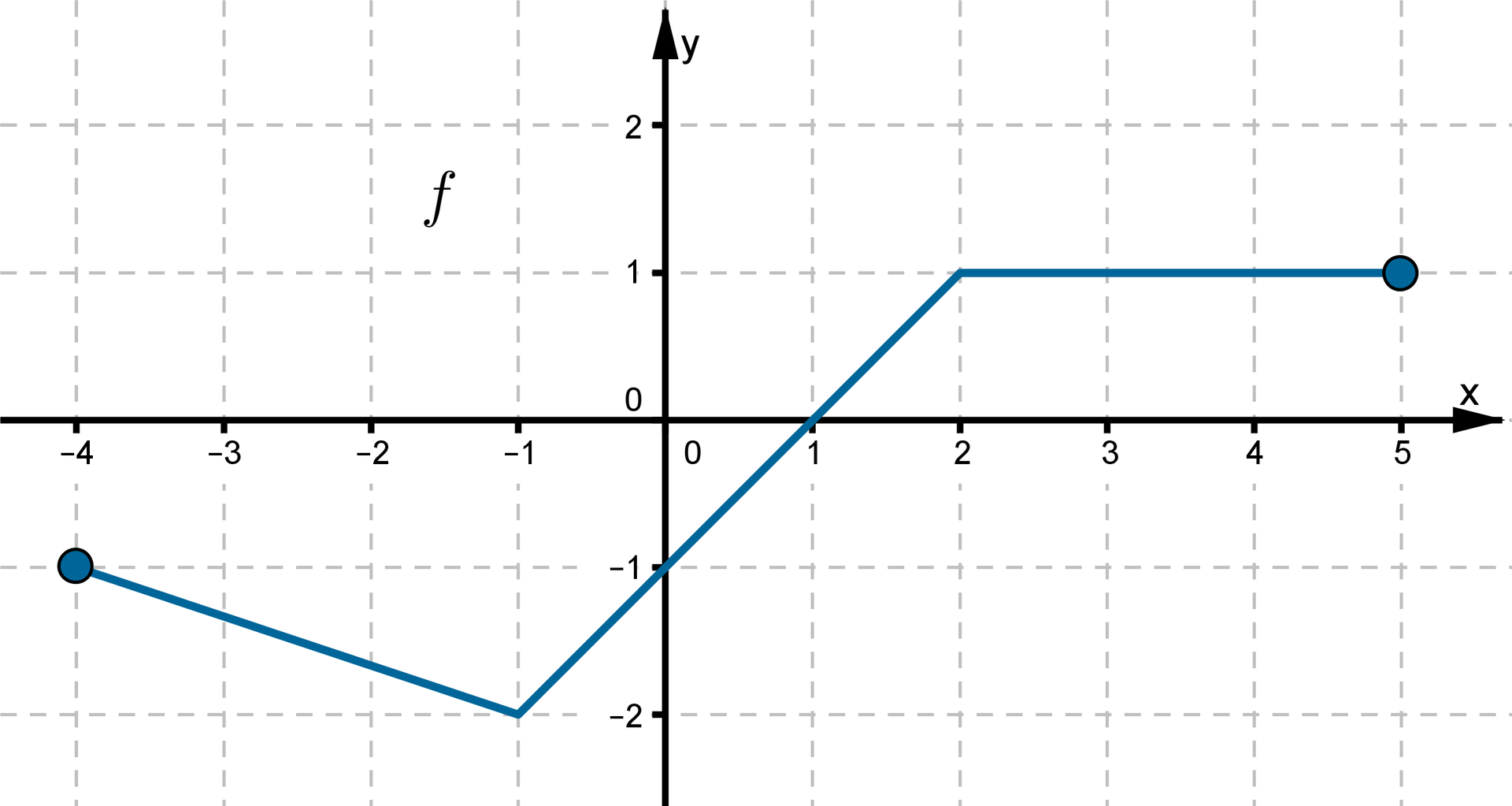
Z wykresu funkcji odczytamy na przykład, że:
w przedziale funkcja jest rosnąca,
w przedziale funkcja jest stała,
w przedziale funkcja jest malejąca.
Zauważmy jednak, że:
przedział jest maksymalnym przedziałem, w którym funkcja jest rosnąca,
przedział jest maksymalnym przedziałem, w którym funkcja jest stała,
przedział jest maksymalnym przedziałem, w którym funkcja jest malejąca,
przedział jest maksymalnym przedziałem, w którym funkcja jest niemalejąca.
Funkcja jest monotoniczna przedziałami, ale nie jest monotoniczna w całym przedziale .